Главная | Обратная связь

Некоторые следствия из аксиом кольца

Определение 2. Разностью элементов а и b из кольца К назовем .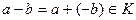

Из аксиом кольца нетрудно получить:

1. .

По определению разности: . Умножим обе части на с:

(a – b)c + bc =ac. Отсюда (a – b)c = ac –- bc (использовалось определение 2).

2. .Действительно, (мы использовали свойство 1).

3. . (9)

, т.е. ; значит, справедливо равенство (3).

Замечание 2. Мы видим, что в кольце выполняются три операции: сложение, вычитание и умножение. Деления в кольце может и не быть. Например, в кольце целых чисел нельзя выполнить деление числа 2 на 4, т.к. результат операции должен быть элементом этого же кольца.

Делители нуля

Определение 3. Пусть К – кольцо. Элементы называются делителями нуля, если , , но .

Во многих кольцах делителей нуля нет; такими являются, например, все числовые кольца, т.е. кольца, содержащиеся в С. Однако, делители нуля есть в кольцах M_n(R) и Ф. Например, матрицы . являются делителями нуля в M_n(R), т.к.

 

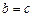Утверждение. В кольце без делителей нуля можно производить сокращения на ненулевые элементы, т.е. если (1) и (2), то . (3)

Доказательство. Из равенства (1) имеем: . В силу дистрибутивного закона для разности отсюда получаем: (4). Т.к. в рассматриваемом кольце по условию нет делителей нуля, то из равенств (4) и (2) следует: , т.е. b=c. Равенство (3) доказано.

Замечание 3. В кольцах с делителями нуля сокращать можно не всегда, даже на ненулевые элементы.

Поля

Определение 1. Кольцо Р называется полем, если

1.P≠0;

2. в Р существует единичный элемент 1;

3. для любого ненулевого элемента а из Р существует обратный элемент а^-1 , т.е. ;

4. умножение коммутативно.

Примеры полей:

1. Множество рациональных чисел Q.

2. Множество действительных чисел R.

3. Множество комплексных чисел C.

4. Множество Р₂={0,1} с новым правилом сложения: 1+1=0 (в остальном сложение и умножение 0 и 1 обычное). Это единственный пока пример конечного поля (поле Р₂ можно представить, как поле из двух элементов – четные числа (0) и нечетные числа (1)).

Определение поля можно дать и более компактно.

Определение 2. Множество Р, в котором определены две алгебраические операции – сложение и умножение, называется полем, если

1..

2. Р – коммутативная группа по сложению.

3. Р\0 – коммутативная группа по умножению.

4. В Р выполняется дистрибутивный закон.