Главная | Обратная связь

Построение поля комплексных чисел на языке подполей и расширений

Проведенное в §1 главы I построение поля С содержало ряд нестрогостей. Сейчас мы их устраним на языке подполей и расширений.

Задача, которую мы ставили при построении комплексных чисел, теперь ставится так: найти расширение поля R с помощью корня уравнения .

Если через i обозначить какой-то корень этого уравнения, то нам нужно найти R(i) – минимальное расширение поля R,

содержащее i.

Решение этой задачи проводим по следующим этапам:

1. Рассмотрим множество С всех точек плоскости XOY. В этом множестве вводим операции сложения, умножения (как в §1 гл.I). Проверяем, что С – поле (выполнение большинства аксиом поля в С в §1 гл.1 проверялось).

2. Во множестве С рассматриваем подмножество , состоящее из всех точек оси ОХ. Проверяем, что S – подполе поля С.

Для этого достаточно убедиться в следующем:

,

.

3. Рассмотрим отображение , т.е. . Проверяем, что φ – изоморфизм полей R и S (это нетрудно), т.е. . На основании этого изоморфизма отождествляем точки оси ОХ и действительные числа, т.е. полагаем: . Получаем, что ; следовательно, С – расширение поля R.

4. Рассмотрим точку 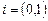, и проверяем, что (в §1 гл.1 это сделано). Как и в §1 гл.1, получаем алгебраическую форму комплексных чисел, т.е. .

5. Проверим, что R(i)=C.

Т.к. и R(i) поле, то из для любых имеем: ,т.к. ; . А тогда . Следовательно, ; но ; значит, .

Поставленная задача решена.

Определители и матрицы над произвольным полем

Можно проверить, что вся теория матриц и теория определителей остаются справедливыми, если в качестве элементов матриц и определителей рассматривать элементы произвольного поля (элементы поля часто называют числами). Отметим, что при этом приходится другим путем доказывать равенство нулю определителя, содержащего две одинаковые строки, ибо в поле характеристики 2 из равенства d=-d не следует, что d=0.

Глава 7. МНОГОЧЛЕНЫ И ИХ КОРНИ

Кольцо многочленов

Определение 1. Назовем многочленом (или полиномом) п-й степени от неизвестного х над полем P формальное выражение вида

a₀xⁿ + a₁x^n-1 +…+ a_n-1x¹ + a_n = f(x) ,

где nÎNÈ0 и коэффициенты a₀ , a₁ ,…, a_n-1, a_n принадлежат полю P, причем старший коэф­фициент a₀ должен быть отличным от нуля.

Выражение вида :

0xⁿ +0x^n-1+…+ 0x¹ +0

назовем нулевым многочленом . Это единственный многочлен, не имеющий степени.

Отметим, что при a₀¹0 a₀x⁰ – многочлен нулевой степени.

Определение 2. Два многочлена f(x) и g(x) назовем равными (или тождественно равными) f(x)=g(x), если равны их коэффициенты при одинаковых степенях неизвестного.

В частности, нулевой многочлен – это число 0 из P. Поэтому никакой многочлен, хотя бы один коэффициент которого отличен от нуля, не может быть равным нулевому многочлену. Отметим, что знак равенства, упо­требляемый в записи уравнения n-й степени f(x)=0, не имеет никакого отношения к определенному сейчас равенству многочленов. Знак равенства, связывающий многочлены, следует в дальнейшем всегда понимать в смысле тождественного равенства этих многочленов.

Если даны многочлены f(x) и g(x) с коэффициен­тами из поля P, записанные для удобства по возрастающим степеням х:

f(x)= a₀ +a₁ x¹+…+ a_n-1 x^n-1+a_n xⁿ , a_n¹0, (1)

g(x)= b₀ +b₁ x¹+…+ b_s-1 x^s-1+b_s x^s , b_s¹0 , (2)

и если, например, n>s , то их суммой называется многочлен

f(x)+g(x)= c₀ +c₁ x¹+…+ c_n-1 x^n-1+c_n xⁿ ,

коэффициенты которого получаются сложением коэффициентов многочленов f(х) и g(x), стоящих при одинаковых степенях неизвест­ного, т. е. c_i =a_i +b_i i = 1, ..., n,

(недостающие степени в записи g(x) добавляем с нулевыми коэффициентами).

Произведением многочленов f(x) и g(x) называется многочлен, коэффициенты которого определяются следующим образом:

f(x)g(x)= d₀ +d₁ x¹+…+ d_n+s-1 x^n+s-1+d_n+s x^n+s , d_n+s¹0 ,

где . (3)

Этот результат получим, подставив в f(x)g(x) их виды (1) и (2), а затем раскрыв скобки и приведя подобные. В частности, d_n+s=a_nb_s. Т.к. a_n¹0, b_s¹0 и в поле нет делителей нуля,то отсюда вытекает, что степень произведения двух ненулевых много­членов равна сумме степеней этих многочленов.

Отсюда следует

Утверждение 1. Произведение многочленов, отличных от нуля, никогда не будет равным нулю.

Обозначим через P[x] множество всех многочленов от x с коэффициентами из P.

Покажем,что P[x] – кольцо:

1) Коммутативность и ассоциативность сложе­ния немедленно вытекают из справедливости этих свойств для сло­жения коэффициентов из поля P, так как складываются коэффициенты при каждой степени неизвестного отдельно. Нулевой многочлен – это число 0ÌP.

2) Противоположным для записанного в (1) много­члена f(x) будет многочлен

-f(x)= -a₀-a₁x¹-…-a_n-1x^n-1-a_nxⁿ , т.к. -a_i ÎP и

f(x)+(-f(x))=0.

3) Коммутативность умножения вытекает из коммутатив­ности умножения коэффициентов из поля P и того факта, что в определении произведения многочленов (смотрите (3)) коэффициенты обоих множителей f(x) и g(x) исполь­зуются совершенно равноправным образом:

.

 

4) Ассоциативность умножения :

[f(x)g(x)]h(x)= f(x)[g(x)h(x)].

Если f(x) записать в виде (1), g(x) – в виде (2), и h(x)= c₀+c₁x¹+…

+c_k-1x^k-1+c_kx^k , то коэффициентом при xⁱ в произведении [f(x)g(x)]h(x) будет число:

, а в произведении f(x)[g(x)h(x)] – число

.

Эти числа равны. Ассоциативность доказана.

5) Роль единицы при умножении многочленов играет число 1, т.к. f(x)×1=f(x).

6) [f(x)+g(x)]h(x) = f(x)h(x)+g(x)h(x).

Дистрибутивность вытекает из равенства:

,

так как левая часть этого равенства является коэффициентом при хⁱ в многочлене [f(x) + g(x)]h(x), а правая часть — коэффициентом при той же степени неизвестного в многочлене f(x) h(x)+g(x)h (x).

Итак, P[x] кольцо. В силу утверждения 1 в нем нет делителей нуля.

Доказана.

Теорема 1. P[x] – кольцо без делителей нуля.

Посмотрим, не будет ли P[x] полем.

Выше отмечено, что роль единицы при умножении многочленов играет число 1, рассматриваемое как многочлен нулевой степени. С другой стороны, многочлен f(x) тогда и только тогда обладает обрат­ным многочленом f ^-1 (x) в P[x]_, f(x)f^-1(x)=1, (5)

когда f(x) является многочленом нулевой степени. Действительно, если f(x) является отличным от нуля числом а, то обратным много­членом служит для него число а^-1ÎP. Если же f(x) имеет степень n>1, то степень левой части равенства (5), если бы многочлен f^-1(х) существовал, была бы не меньше п, в то время как справа стоит многочлен нулевой степени.

Отсюда вытекает, что не всякий многочлен имеет в Р[x] обратный. Поэтому кольцо P[x] не является полем. В этом отношении (и, как мы увидим, во многих других) кольцо P[x] напоминает кольцо Z целых чисел.

Замечание. Многочлены из P[x] можно рассматривать и как функции, заданные на P. Но понятия равенства функций (f(x)=g(x)Ûf(x₀)=g(x₀) x₀ÎP) отличается от понятия равенства многочленов (как тождественного равенства). В дальнейшем мы получим равносильность двух понятий равенства – алгебраического и теоретико-функционального, но только для бесконечных полей. В общем случае эти понятия не совпадают.

Пример. Рассмотрим многочлены f(x)=x²+1 и g(x)=x+1 над полем P={0,1} из двух элементов. Имеем: f(1)=1²+1=0; g(1)=1+1=0; f(0)=0²+1=1; g(0)=0+1=1.

Итак, g(x₀)=f(x₀) "x₀ÎP, т.е. f(x) и g(x) – равные функции, но как многочлены они не равны.

Деление с остатком

Мы отмечали, что у колец P[x] и Z много общего.

Аналогия P[x] и Z проявляется и в том, что для многочленов, как и для целых чисел, существует алгоритм деле­ния с остатком. Этот алгоритм для случая многочленов с дей­ствительными коэффициентами известен еще из элементар­ной алгебры. Так как, однако, мы рассматриваем теперь случай многочленов с коэффициентами из любого поля, следует дать заново все относящиеся сюда формулировки и привести доказательства.

Теорема 1. Для любых двух многочленов f(x) и g(x) из P[x] при g(x)¹0 можно найти такие многочлены q(x) и r(x) из P[x], что

f(x)=g(x)q(x) + r(x), (6)

причем или степень r (х) меньше степени g(x), или же r(х) = 0. Многочлены q(x) и r(х), удовлетворяющие этому условию, опре­деляются однозначно.

Доказательство. Докажем сначала вторую половину теоремы. Пусть существуют еще многочлены и , также удовлетворяющие равенству

f(x)=g(x) + , (7)

, ÎP[x],

причем степень снова меньше степени g(x). Приравнивая друг другу правые части равенств (6) и (7), получим:

Степень правой части этого равенства меньше степени g(x), степень же левой части была бы при больше или равна сте­пени g(x) (мы учитываем, что g(x)¹0). Поэтому должно быть =0 т. е. , а тогда и r(х) = (х), что и требовалось доказать.

Переходим к доказательству первой половины теоремы. Если f(x)=0,то f(x)=0×g(x)+0. Пусть многочлены f(x) и g(x) имеют, соответственно, степени п и s. Если п<s, то можно положить q(x)=0, r(x)=f(x). Если же п≥s, то воспользуемся тем же методом ”деления столбиком”, каким в элементарной алгебре производилось деление многочленов с действительными коэффициен­тами, расположенных по убывающим степеням неизвестного. Пусть

f(x)=a₀xⁿ+a₁x^n-1+…+a_n-1x+a_n, a₀¹0,

g(x)=b₀x^s+b₁x^s-1+…+b_s-1x+b_s, b₀¹0.

Полагая

Î P[x], (8)

мы получим многочлен, степень .которого меньше п. Обозначим эту степень через n₁, а старший коэффициент многочлена f₁(х) – через а₁₀. Положим, далее, если все еще n₁≥s₁

Î P[x], (8₁)

обозначим через n₂ – степень, а через а₂₀ – старший коэффициент многочлена f₂ (x)_t; положим затем

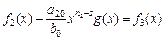Î P[x] (8₂)

и т. д.

Так как степени многочленов f₁ (x),f₂ (х), ,,, убывают. п≥n₁≥n₂≥ ..., то мы дойдем после конечного числа шагов до такого многочлена f_к(х),

Î P[x], (8_k-1)

степень которого n_k меньше s, после чего наш процесс останавливается. Складывая теперь равенства (8), (8₁), ..., (8_k-1), мы получим:

Î P[x],

т. е. многочлены q(x)= 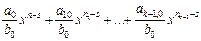и r(x)=f_k(x) из P[x] действительно удовлетворяют равенству (6), причем степень r(х) меньше степени g(x).

Теорема доказана.

Замечание. Многочлен q(х) называется частным от деления f(х) на g(x), а r(х) –остатком от этого деления.