Главная | Обратная связь

Свойства делимости многочленов

Все многочлены, о которых говорится в свойствах делимости, принадлежат P[x]. Элементы поля P мы назовем числами.

I. Если f(х) делится на g(x), a g(x) делится на h(x), то f(x) будет делиться на h(x).

В самом деле, по условию f(x) = g(х) (х) и g(x)=h(x) (x), а поэтому f(x) = h(x)[ (x) (x)].

П. Если f(x) и g(x) делятся на (х), то их сумма и раз­ность также делятся на (x).

Действительно, из равенств f(x)= (x) (х) и g(х) = (х) (х) вытекает f(x)±g (х)= (х) [ (х) ± (х)].

Ш. Если f(x) делится на (x), то произведение f(x) на любой многочлен g(x) также будет делиться на (x).

Действительно, если f(x) = (x) (х) ,то f(x)g (х) = (х)[ (x)g(x)].

Из II и III вытекает следующее свойство:

IV. Если каждый из многочленов f₁(х), f₂(х), ..., f_k(x) делится на (х), то на (х) будет делиться и многочлен

f₁(х)g₁(x)+ f₂(х)g₂(x)+ ...+ f_k(x)g_k(x), где g₁ (x), g₂ (х),..., g_k (x) — произвольные многочлены.

V. Всякий многочлен f(x) делится на любой многочлен нулевой степени.

Если f(x)=a₀xⁿ+а₁x^n-1+…+a_n и с – произвольное число из поля P, не равное нулю, т. е. произвольный многочлен нулевой степени, то .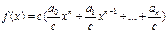

Замечание 1. Многочлены нулевой степени – это все многочлены из P[x], имеющие обратные. В кольце Z этим свойством обладают только числа (±1). Поэтому аналогичное V свойство кольца Z – всякое целое число делится на (±1), и других целых чисел, на которые все целые делятся, нет.

VI. Еcли f(x) делится на (x), то f(х) делится и на c (х), где с – элемент поля P , отличный от нуля.

В самом деле, из равенства f(x) = (x) (x) следует равенство

f(x)=[c (x)][c^-1 ].

VII. Многочлены сf(x), с¹0, и только они будут делителями
многочлена f(x), имеющими такую же степень, что и f(x).

На самом деле, f(x) = c^-1[cf(x)], т. е. f(x) делится на сf(х).

Если, с другой стороны, f(x) делится на (x), причем степени f(x) и (х) совпадают, то степень частного от деления f(x) на (x) должна быть равной нулю, т. е. f(x)=d (x), d¹0, откуда

(x)=d^-1f(x).

Отсюда вытекает следующее свойство:

VIII. Тогда и только тогда многочлены f(x)_, g(x) одновременно
делятся друг на друга, когда g(x)=cf(x), c¹0 (для целых чисел: два целых числа тогда и только тогда делятся друг на друга, когда они отличаются только множителем (±1)) .

Наконец, из VIII и I вытекает свойство

IX. Всякий делитель одного из двух многочленов f(x), cf(x),
где c¹0, будет делителем и для другого многочлена.

Замечание 2. Благодаря отмеченным выше связям свойств делимости многочленов и целых чисел многим утверждениям для Z, в которые входит фраза “с точностью до знака”, в P[x] соответствует фраза “с точностью до множителей нулевой степени”.