Главная | Обратная связь

Многочлены с действительными коэффициентами

Теорема 7. Если комплексное (но не действительное) число служит корнем многочлена f(x) с действительными коэффициен­тами, то корнем для f(x) будет и сопряженное число 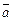, причем эти корни будут иметь одну и ту же кратность.

Доказательство. Пусть многочлен с действительными коэффи-циентами f(x) = c₀xⁿ +c₁x^n-1+…+ c_n-1x¹ +c_n имеет комплексный корень . Тогда

.

Мы знаем, что последнее равенство не нарушится, если в нем все числа заменить на сопряженные. Однако все коэффициенты с_i, а также число 0, стоящее справа, будучи действи­тельными, останутся при этой замене без изменения, и мы приходим к равенству

, т. е. . Значит, 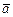– также корень f(x).

Так как , то многочлен f(x) будет делиться на квадратный трехчлен

g(х) = = 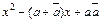, (1)

коэффициенты которого действительны. Пользуясь этим, докажем, что корни и 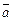имеют в многочлене f(x) одну и ту же кратность.

Пусть эти корни имеют, соответственно, крат­ности k и t и пусть, например, k>t. Тогда f(x) = 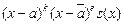=g^t(x)q(x), где q(x)=(x-a)^k-ts(x), (2)

причем s(x) не имеет корней a и 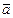. Поэтому q( 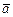)¹0. (3)

Многочлен q(x), как частное двух многочленов с действительными коэффициентами, также имеет действительные коэффициенты. В силу (2) он имеет число своим корнем, тогда как число 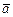(в силу (3)) не является его корнем, в противоречие с доказанным выше. Отсюда следует, что k = t.

Таким образом, теперь можно сказать, что комплексные корни всякого многочлена с действительными коэффициентами попарно сопряжены. Отсюда и из разложения (1) из §8, в силу его единственности (следствие 1 теоремы 5) вытекает следующий результат:

Следствие 1. Всякий отличный от нуля многочлен f(x) с действительными коэффициентами представим, притом единственным способом (с точностью до порядка множителей), в виде произведения своего старшего коэф­фициента а₀ и многочленов с действительными коэффициентами: линейных вида х-с_i, соответствующих его дей­ствительным корням, и квадратных вида (1), соответствующих парам сопряженных комплексных корней.

Следствие 2. Всякий отличный от нуля многочлен f(x) с действительными коэффициентами представим (однозначно) в виде

f(x)= , где 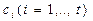– все различные действительные корни f(x), , где (j = 1,..,s) – все различные недействительные корни f(x).

Такое разложение называют каноническим разложением многочлена с действительными коэффициентами над полем R.

Справедливость этого утверждения вытекает из следствия 1.

Следствие 3. Число недействительных корней отличного от нуля многочлена с действительными коэффициентами всегда четно.

Следствие 4. Многочлен нечетной степени с действительными коэффициентами имеет хотя бы один действительный корень.