 |
|
Некоторые следствия из аксиом линейного пространства
Следствие 1. Пусть L – линейное пространство над полем Р. В L содержится нулевой элемент 0 и"аÎL (-а)ÎL (т.к. L – группа по сложению).
В дальнейшем нулевой элемент поля Р и линейного пространства L будем обозначать одинаково - через 0. Путаницы это обычно не вызывает.
Следствие 2. 0×a=0 "aÎL (в левой части 0ÎP, в правой 0ÎL).
Доказательство. Рассмотрим α×a, где α — любое число из Р. Имеем: α×a=(α+0)a=α×a+0×a, откуда 0×a= α×a +(-α×a)=0.
Следствие 3. α×0=0 "αÎP.
Доказательство. Рассмотрим α×a=α(a+0)=α×a+α×0; отсюда α×0=0.
Следствие 4. α×a=0 тогда и только тогда, когда либо α=0, либо а=0.
Доказательство. Достаточность доказана в следствиях 2 и 3.
Докажем необходимость. Пусть α×a=0 (2). Предположим, что α×¹0. Тогда, т.к.αÎP, то существует α-1ÎP. Домножая (2) на α-1, получаем:
α-1(α×a)=α-1×0. По следствию 2 α-1×0=0, т.е. α-1(α×a)=0. (3)
С другой стороны, пользуясь аксиомами 2 и 5 линейного пространства, имеем: α-1(α×a)=(α-1α)×a=1×a=a. (4)
Из (3) и (4) следует, что а=0.
Следствие доказано.
Следующие утверждения приведем без доказательства (их справедливость легко проверяется).
Следствие 5.(-α)×a=-α×a "αÎP, "aÎL.
Следствие 6. α×(-a)=-α×a "αÎP, "aÎL.
Следствие 7. α×(a–b)=α×a–α×b "αÎP, "a,bÎL.
Линейная зависимость векторов
Пусть L – линейное пространство над полем P и a1,a2,…as (1) – некоторое конечное множество векторов из L.
Множество a1,a2,…as будем называть системой векторов.
Если b = α1a1+α2a2+…+αsas, (αiÎP), то говорят, что вектор b линейно выражается через систему (1), или является линейной комбинацией векторов системы (1).
Как и в аналитической геометрии, в линейном пространстве можно ввести понятия линейно зависимых и линейно независимых систем векторов. Сделаем это двумя способами.
Определение I. Конечная система векторов (1) при s³2 называется линейно зависимой, если хотя бы один ее вектор является линейной комбинацией остальных. В противном случае (т.е. когда ни один ее вектор не является линейной комбинацией остальных), она называется линейно независимой.
Определение II. Конечная система векторов (1) называется линейно зависимой, если существует набор чисел α1,α2,…,αs, αiÎP,хотя бы одно из которых не равно 0 (такой набор называют ненулевым), что выполняется равенство: α1a1+…+αsas=0 (2).
Из определения II можно получить несколько равносильных определений линейно независимой системы:
Определение 2.
a) система (1) линейно независима, если из (2) следует, что α1=…=αs=0.
b) система (1) линейно независима, если равенство (2) выполняется только при всех αi=0 (i=1,…,s).
c) система (1) линейно независима, если любая нетривиальная линейная комбинация векторов этой системы отлична от 0, т.е. если β1, …,βs – любой ненулевой набор чисел, то β1a1+…βsas¹0.
Теорема 1. При s³2 определения линейной зависимости I и II равносильны.
Доказательство.
I) Пусть (1) линейно зависима по определению I. Тогда можно считать, не нарушая общности, что as=α1a1+…+αs-1as-1. Прибавим к обеим частям этого равенства вектор (-as). Получим:
0= α1a1+…+αs-1as-1+(-1)×as (3) (так как по следствию 5
(–as) =(-1)×as). В равенстве (3) коэффициент (-1)¹0, и потому система (1) линейно зависима и по определению II.
II) Пусть система (1) линейно зависима по определению II, т.е. существует ненулевой набор α1,…,αs, что выполняется (2). Не нарушая общности, можно считать, что αs¹0. В (2) к обеим частям прибавим (-αs×as). Получим:
α1a1+α2a2+…+αsas- αsas= -αsas, откуда α1a1+…+αs-1as-1= -αsas. (4)
Т.к. αs¹0, то существует αs-1ÎP. Умножим обе части равенства (4) на (-αs-1) и воспользуемся некоторыми аксиомами линейного пространства. Получаем:
(-αs-1)×(-αsas)= (-αs-1)( α1a1+…+αs-1as-1), откуда следует:
(-αs-1α1)×a1+…+(-αs-1)×αs-1as-1=as.
Введем обозначения β1= -αs-1α1,…, βs-1=(-αs-1)×αs-1. Тогда полученное выше равенство перепишется в виде:
as= β1×a1+…+ βs-1as-1.
Так как s³2, то в правой части будет хотя бы один вектор ai. Мы получили, что система (1) линейно зависима по определению I.
Теорема доказана.
В силу теоремы 1 при необходимости при s³2 мы можем применять любое из данных выше определений линейной зависимости.
Замечание 1.Если система состоит только из одного вектора а1, то к ней применимо только определение II.
Пусть а1=0; тогда 1×а1=0. Т.к. 1¹0, то а1=0 - линейно зависимая система.
Пусть а1¹0; тогда α1×а1≠0, при любом α1¹0. Значит, ненулевой вектор а1 – линейно независимая система.
Существуют важные связи между линейной зависимостью системы векторов и ее подсистем.
Теорема 2. Если некоторая подсистема (т.е. часть) конечной системы векторов линейно зависима, то и вся система линейно зависима.
Доказательство этой теоремы нетрудно провести самостоятельно. Его можно найти в любом учебнике по алгебре или аналитической геометрии.
Следствие 1. Все подсистемы линейно независимой системы линейно независимы.
Получается из теоремы 2 методом от противного.
Замечание 2. Нетрудно видеть, что у линейно зависимых систем подсистемы могут быть как линейно зависимые, так и линейно независимые.
Пример. На рис.1 a1, a2, a3 - линейно зависимая система.
a1, a2- ее линейно зависимая подсистема, Рис.1
a1, a3 - ее линейно независимая подсистема.
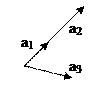
 Рис. 1
Рис. 1
Следствие 2.Если система содержит 0 или два пропорциональных (равных) вектора, то она линейно зависима (так как подсистема из 0 или двух пропорциональных векторов линейно зависима).