 |
|
Неприводимые и приводимые
Многочлены над полями C и R
Ниже мы введем понятие многочленов, играющих в теории многочленов ту же роль, что простые числа играют в теории целых чисел.
Простое число нельзя разложить в произведение двух множителей, меньших по модулю. Аналогично определяются неприводимые многочлены, только вместо модулей рассматриваются степени многочленов.
Определение 1.Многочлен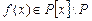 
(где P – произвольное поле) называют приводимым над полем P, если он представим в виде 
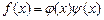(1), где 
, 
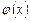(2), причем 
, 
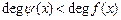. В противном случае 
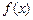называется неприводимым над полем P.
Из определения видно, что элементы поля P мы не относим ни к приводимым, ни к неприводимым многочленам (аналогично числа 
– ни простые, ни составные).
Замечание 1. Другими словами, многочлен 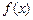, не содержащийся в поле P, называется неприводимым над P, если в любом его разложении вида (1) с условием (2) степень хотя бы одного из множителей – нулевая (а степень второго равна степени 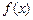). Неприводимый многочлен 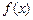над P нельзя разложить в произведение двух множителей из 
степеней, меньших, чем степень .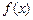
Пример. Многочлен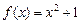 
над полем R неприводим, а над С – приводим, ибо 
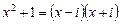, где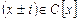 
.
Замечание 2. Если многочлен приводим над P, то при расширении поля P, он, очевидно, остается приводимым.
С другой стороны, как показывает приведенный выше пример, неприводимый многочлен над P при расширении поля до 
может стать приводимым над .
Лемма 1. Многочлен первой степени неприводим над любым полем.
Доказательство. Пусть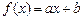 
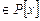и 
.
Предположим, что 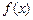приводим над 
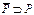; тогда 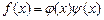, где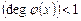 
, 
. Отсюда следует, что 
, 
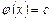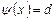и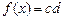 
, 
.
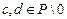В последнем равенстве слева стоит многочлен первой степени, а справа – нулевой степени. Такое равенство невозможно. Полученное противоречие доказывает лемму.
Найдем все неприводимые многочлены над полями C и R.