Главная | Обратная связь

Длина вектора. Угол между векторами

Определение 1. Нормой, или длиной, вектора а евклидова пространства V называется число |а| = (корень берется арифметический).

Часто норма обозначается так: ||a||.

Отметим, что так как (а, а)³0, то длина вектора всегда существует. Если |а|=0, то а=0, и обратно.

Определение 2. Если |е|=1, то вектор е называется нормированным вектором или ортом.

Покажем, что любой ненулевой вектор можно нормировать, если его разделить на его длину. Действительно, . Введем обозначение: = е. Тогда (е, е)=1, т.е. е – орт.

Определение 3. Базис е₁,…,е_n (1) евклидова пространства V_n называется ортонормированным, если он состоит из попарно ортогональных ортов, т.е. для любых i, j=1,...,n (e_i, e_j)=0 (2) при i j и (e_i, e_i)=1 (3).

Теорема 3.Во всяком конечномерном евклидовом пространстве V_n существует ортонормированный базис.

Доказательство. Рассмотрим ортогональный базис b₁,...,b_n (4) пространства V_n (он существует в силу следствия 1 теоремы 2) и нормируем каждый его вектор. Получим: е₁,…,е_n (5), где 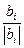= е_i. Нетрудно проверить, что система (5) останется ортогональной, так как если (c, d)=0, то для любых a, b из R справедливо равенство (ac, bd)= ab (c, d)=0, т.е. векторы ac и bd также ортогональны.

Система (5) – это n попарно ортогональных ненулевых векторов. Она по теореме 1 линейно независима, и так как n=dim V_n, то (5) – базис V. Это искомый ортонормированный базис.

Теорема доказана.

Замечание 1. Ниже в конечномерных евклидовых пространствах мы будем выбирать только ортонормированные базисы.

По аналогии с геометрией на плоскости в любом евклидовом пространстве можно ввести понятие угла между векторами.

Определение 4.Углом между ненулевыми векторами х и у евклидова пространства V называют угол j, определяемый соотношениями.

Корректность определения угла вытекает из неравенств , равносильных неравенству Коши – Буняковского: .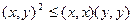

Доказательство (этого неравенства). По определению скалярного произведения для любых векторов х и у из V и любого действительного числа a выполняется неравенство . Из него получаем: . Левая часть последнего неравенства представляет собой квадратный трехчлен относительно a. Поскольку этот трехчлен неотрицательный, его дискриминант меньше или равен нулю, т.е. .

Неравенство Коши – Буняковского доказано.

Следствие. Для любых двух векторов x и y евклидова пространства V справедливо неравенство треугольника .

Доказательство. Действительно, раскрывая величину как скалярный квадрат и учитывая, что в силу неравенства Коши – Буняковского 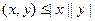, находим: .

Так как числа и неотрицательные, то отсюда вытекает справедливость неравенства треугольника.

Следствие доказано.