 |
|
ГЛАВА 3. НЕКОТОРЫЕ ВИДЫ ЛИНЕЙНЫХ ПРЕОБРАЗОВАНИЙ ЕВКЛИДОВЫХ ПРОСТРАНСТВ
§1. Ортогональные матрицы
Мы рассмотрим некоторые полезные виды линейных преобразований евклидовых пространств и связанные с ними матрицы.
Определение 8. Квадратная действительная матрица А, для которой А’=А-1, называется ортогональной матрицей.
Примеры. Е,  ,
,  .
.
Теорема 1.Множество Q всех ортогональных матриц n-ого порядка составляет группу по умножению.
Доказательство. Проверим сначала замкнутость умножения в Q.
Пусть А и В содержатся в Q. Тогда по определению 8 А’=A-1 (1), B’=B-1 (2). Рассмотрим (AB)’. Имеем (AB)’=B’A’=В-1А-1=(АВ)-1 (мы использовали равенства (1) и (2)). Следовательно, АВÎQ. Далее, EÎQ. Наконец, если AÎQ, из (1) следует: (А-1)-1=А=(А’)’=(A-1)’. Поэтому  ÎQ. Значит, Q – группа.
ÎQ. Значит, Q – группа.
Теорема доказана.
Свойства ортогональных матриц
1.Если А – ортогональная матрица, то АА’=A’A=E (3). Это свойство, очевидно, равносильно определению 8.
2.Если AÎQ, то |A|=  1. Действительно из (3) следует: |AA’|=|A||A’|=|A|2=|E|=1. Значит, |A|=
1. Действительно из (3) следует: |AA’|=|A||A’|=|A|2=|E|=1. Значит, |A|=  1. В частности, всякая ортогональная матрица невырожденная.
1. В частности, всякая ортогональная матрица невырожденная.
Следующие важные свойства ортогональных матриц докажем в теореме 2.
Теорема 2.Пусть дана действительная матрица А=  .
.
А является ортогональной тогда и только тогда, когда выполняются равенства:  (4) и
(4) и  (5) при i
(5) при i  j.
j.
Необходимость. Пусть АÎQ. Тогда по свойству 1 АА’=Е
 (6). Значит, верны равенства (4) и (5).
(6). Значит, верны равенства (4) и (5).
Достаточность. Пусть выполняются равенства (4) и (5).Тогда, очевидно АА’=Е, и поэтому А’=А-1, т.е. А – ортогональная матрица.
Теорема доказана.
Замечание 1.Нетрудно доказать (используя равенство АА’=Е), что свойства, аналогичные (4) и (5) для столбцов матрицы А, также равносильны определению ортогональной матрицы.
Теорема 3.Матрица перехода от одного ортонормированного базиса е к другому ортонормированному базису е’ конечномерного евклидова пространства Vn является ортогональной матрицей.
Доказательство.  . Т=(τkj) – матрица перехода от е в е’. Так как е – ортонормированный базис, то скалярное произведение векторов в нем равно сумме произведений соответствующих координат. Учитывая это и то, что е’ – ортонормированный базис, получаем: (ei’,ei’)=
. Т=(τkj) – матрица перехода от е в е’. Так как е – ортонормированный базис, то скалярное произведение векторов в нем равно сумме произведений соответствующих координат. Учитывая это и то, что е’ – ортонормированный базис, получаем: (ei’,ei’)=  =1 (6) и (ei’,ej’)=
=1 (6) и (ei’,ej’)=  =0 (7) при i
=0 (7) при i  j. Из (6) и (7), в силу замечания 1 к теореме 2, следует, что Т – ортогональная матрица.
j. Из (6) и (7), в силу замечания 1 к теореме 2, следует, что Т – ортогональная матрица.
Теорема доказана.
§2. Сопряженные линейные преобразования
В связи с наличием скалярного произведения в евклидовых пространствах можно выделить специальные виды линейных преобразований таких пространств. Мы рассмотрим:
1) сопряженные преобразования;
2) ортогональные преобразования;
3) симметричные преобразования.
Определение 9. Пусть V – евклидово пространство и φ – его линейное преобразование. Линейное преобразование φ* пространства V называется сопряженным с φ, если для любого вектора а из V справедливо равенство: (φ(a),b)=(a, φ*(b)). (1)
Теорема 1.Пусть линейное преобразование φ конечномерного евклидова пространства Vn имеет в некотором ортонормированном базисе е матрицу А. Тогда линейное преобразование φ*, имеющее в этом же базисе матрицу А’, является сопряженным с φ.
Доказательство. Надо проверить для такого φ* справедливость равенства (1). Пусть [a], [b], [φ(a)], [φ*(b)] – координатные столбцы векторов, стоящих внутри скобок, в базисе е. Тогда, как известно, [φ(a)]=A[a] (2), [φ*(b)]=A’[b] (3). Так как базис е ортонормированный, то (φ(a),b)=[φ(a)]’[b]=(A[a])'[b]=[a]’A’[b] (4). С другой стороны, (a,φ*(b))=[a]’A’[b] (5). Из (4) и (5) следует (1).
Теорема доказана.
Замечание 1.Из данного способа нахождения φ* не видно, будет ли у φ единственное сопряженное преобразование. Однако это легко получается из следующей леммы.
Лемма 1.Пусть φ и ψ – линейные преобразования евклидова пространства, удовлетворяющие для любых a, b Î V условиям: (a, φ(b))=(a, ψ(b)) (6). Тогда φ = ψ.
Доказательство. Из равенства (6) и свойств скалярного произведения следует: (a,(φ- ψ)b)=0 (7). В частности, взяв a=(φ- ψ)b, получим: ((φ- ψ)b,(φ- ψ)b)=0. Следовательно, (φ- ψ)b=0, т.е. φb = ψb для любого b Î V. Значит, φ = ψ.
Лемма доказана.
Следствие.У всякого линейного преобразования φ конечномерного евклидова пространства  существует единственное сопряженное преобразование.
существует единственное сопряженное преобразование.
Доказательство. Существование доказано в теореме 1. Докажем единственность.Пусть наряду с равенством (1) выполняется равенство (φ(a),b)=(a, ψ (b)) (8). Из (1) и (8) следует, что (a, φ*(b)) = (a, ψ (b)). По лемме 1 φ* = ψ.
Следствие доказано.
Замечание 2.Равенство (1) можно переписать в виде (φ*(b),a)=(b,φ(a)). Значит, (φ*)*= φ, поэтому φ и φ* – взаимно сопряженные преобразования.
§3. Ортогональные преобразования
Определение 10. Линейное преобразование φ евклидова пространства V называется ортогональным, если оно сохраняет скалярное произведение, т.е. для любого а,b  V справедливо равенство: (φ(а), φ(b))=(a,b).
V справедливо равенство: (φ(а), φ(b))=(a,b).
Примеры. Ортогональными преобразованиями плоскости R2 являются поворот плоскости, симметрия относительно оси.
Теорема 1.Линейное преобразование φ евклидова пространства V тогда и только тогда является ортогональным преобразованием, когда φ*=φ-1.
Достаточность. Пусть φ*=φ-1. Тогда (φ(а), φ(b))= (а, φ*φ(b)) =
(а, φ-1 φ(b)) = (а, ε(b))=(a,b), т.е. φ – ортогональное преобразование.
Необходимость. Пусть φ – ортогональное преобразование. Тогда по определению 10 (φ(а), φ(b))=(a,b). Отсюда и из определения сопряженного преобразования следует: (φ(а), φ(b))= (а, φ*( φ(b))) = (а, φ*φ(b))= (a,b)=(а, ε(b)), для любого а, b  V. Тогда по лемме 1 φ φ*= ε. Значит, φ*=φ-1 .
V. Тогда по лемме 1 φ φ*= ε. Значит, φ*=φ-1 .
Теорема доказана.
Теорема 2.Ортогональное преобразование φ конечномерного евклидова пространства Vn переводит любой ортонормированный базис е1,…,еn (1) в ортонормированный базис.
Доказательство. Рассмотрим систему векторов φ(е1),…, φ(еn) (2). Так как φ – ортогональное преобразование, то (φ(еi), φ(еi))= (еi , еi)=1 (3) и (φ(еi), φ(еj))= (еi , еj)=0, где i≠j (мы исходили из того, что базис (1) ортонормированный). Значит, (2) – ортонормированная система n векторов n-мерного евклидова пространства Vn. Так как φ(еi) ≠0 (в силу (3)), то система (2) линейно независима, а значит, является базисом Vn.
Теорема доказана.
Справедлива и обратная теорема.
Теорема 3.Если линейное преобразование φ конечномерного евклидова пространства Vn переводит некоторый ортонормированный базис е=(е1,…,еn) в ортонормированный базис е'=(е'1,…,е'n), то φ является ортогональным преобразованием.
Доказательство. Пусть  и
и 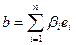 – любые векторы из Vn. Так как е – ортонормированный базис, то
– любые векторы из Vn. Так как е – ортонормированный базис, то  (4). По условию φ(еi)= еi'. Тогда
(4). По условию φ(еi)= еi'. Тогда  ,
,  . Так как е' – ортонормированный базис, то
. Так как е' – ортонормированный базис, то  (5).
(5).
Сравнивая (5) и (4), получаем, что (φ(а), φ(b))=(a,b). Следовательно, φ – ортогональное преобразование.
Теорема доказана.
Теорема 4(о матрицах ортогонального преобразования).Ортогональное преобразование φ конечномерного евклидова пространства Vn в любом ортонормированном базисе имеет ортогональную матрицу.
Доказательство. Пусть е – любой ортонормированный базис Vn, А – матрица преобразования φ в базисе е. В силу теоремы 1 §2 и следствия леммы 1, φ* имеет в этом базисе матрицу А'; но φ-1 имеет матрицу А-1. По теореме 1 §3 φ*= φ-1. Следовательно, А'= А-1 (6), что означает, что матрица А является ортогональной матрицей.
Теорема доказана.
Справедлива и обратная теорема.
Теорема 5.Если линейное преобразование φ евклидова пространства Vn в некотором ортонормированном базисе Vn имеет ортогональную матрицу, то φ – ортогональное преобразование.
Доказательство. Пусть линейное преобразование φ имеет в ортонормированном базисе е ортогональную матрицу А, т.е. А'= А-1. Тогда φ*=φ-1 и по теореме 1 этого параграфа φ – ортогональное преобразование Vn.
Теорема доказана.
§4. Симметрические преобразования
Определение 11. Линейное преобразование φ евклидова пространства V называется симметрическим, если φ = φ*, т.е. для любых векторов a, b  V выполняется равенство: (φ(а), b) = (а, φ(b)).
V выполняется равенство: (φ(а), b) = (а, φ(b)).
Пример. Преобразование растяжения: φ(а)=aа для любого а  V. Тогда (φ(а), b) =(aа, b)= a (а, b)=(а, ab)= (а, φ(b)).
V. Тогда (φ(а), b) =(aа, b)= a (а, b)=(а, ab)= (а, φ(b)).
Определение 12.Квадратная матрица называется симметрической, если она совпадает с транспонированной.
Теорема 1.Симметрическое преобразование конечномерного евклидова пространства Vn в любом ортонормированном базисе имеет симметрическую матрицу.
Действительно, из φ = φ* следует A=A’, т.е. А – симметрическая матрица.
Справедлива и обратная теорема.
Теорема 2. Если линейное преобразование φ конечномерного евклидова пространства Vn имеет в некотором ортонормированном базисе симметрическую матрицу A, то φ – симметрическое преобразование.
В самом деле, из A=A’ следует, что φ = φ*, т.е. φ – симметрическое преобразование.
Теорема 3.Все характеристические корни симметрической матрицы являются действительными числами.
Доказательство. Пусть l0 – характеристический корень (быть может, комплексный) симметрической матрицы А=(aij), т.е. |A-l0E|=0. Тогда система линейных однородных уравнений с комплексными коэффициентами  , i=1,2,…,n, имеет равный нулю определитель, т.е. обладает ненулевым решением b1, b2, …, bn, вообще говоря, комплексным; таким образом,
, i=1,2,…,n, имеет равный нулю определитель, т.е. обладает ненулевым решением b1, b2, …, bn, вообще говоря, комплексным; таким образом,  , i=1,…,n. (1)
, i=1,…,n. (1)
Умножая обе части i-го из равенств (1) на число  , сопряженное с числом
, сопряженное с числом  , и складывая отдельно левые и правые части всех получающихся равенств, мы приходим к равенству
, и складывая отдельно левые и правые части всех получающихся равенств, мы приходим к равенству  . (2)
. (2)
Коэффициент при l0 в (2) является отличным от нуля действительным числом, будучи суммой неотрицательных действительных чисел, хотя бы одно из которых строго положительно. Действительность числа l0 будет поэтому доказана, если мы докажем действительность левой части равенства (2), для чего достаточно показать, что это комплексное число совпадает со своим сопряженным.
Здесь впервые будет использована симметричность (действительной) матрицы А. Имеем: 
 . Заметим, что предпоследнее равенство получено простой переменой обозначений для индексов суммирования: вместо i поставлено j, вместо j поставлено i.
. Заметим, что предпоследнее равенство получено простой переменой обозначений для индексов суммирования: вместо i поставлено j, вместо j поставлено i.
Теорема доказана.
Следствие 1.Все характеристические корни симметрического преобразования φ конечномерного евклидова пространства Vn действительны, т.е. являются его собственными значениями.
Доказательство. Характеристические корни симметрического преобразования по определению совпадают с характеристическими корнями матрицы этого преобразования в некотором базисе, т.е. действительны по теореме 3. Но по теореме о связи между характеристическими корнями и собственными значениями линейного преобразования действительного линейного пространства действительные характеристические корни φ – это и есть собственные значения φ.
Следствие 2.Любое симметрическое преобразование φ конечномерного евклидова пространства Vn имеет хотя бы один собственный вектор (ибо если существует собственное значение линейного преобразования φ, то по определению существует в Vn и собственный вектор этого преобразования).
§5. Основная теорема о симметрических преобразованиях
Теорема 1.Пусть φ – симметрическое преобразование евклидова пространства V, H – подпространство пространства V, инвариантное относительно φ. Тогда его ортогональное дополнение Н┴ в V также инвариантно относительно φ.
Доказательство. Пусть a  H, b
H, b  Н┴. Значит, (а, b)=0 для любых а, b. Так как по условию Н инвариантно относительно φ, то φ(а)
Н┴. Значит, (а, b)=0 для любых а, b. Так как по условию Н инвариантно относительно φ, то φ(а)  H. Следовательно, (φ(а), b)=0. Так как φ – симметрическое преобразование, то (а, φ(b))= (φ(а), b)=0. Значит, φ(b)
H. Следовательно, (φ(а), b)=0. Так как φ – симметрическое преобразование, то (а, φ(b))= (φ(а), b)=0. Значит, φ(b)  Н┴ и Н┴ инвариантно относительно преобразования φ.
Н┴ и Н┴ инвариантно относительно преобразования φ.
Теорема доказана.
Теорема 2(основная теорема о симметрических преобразованиях). Линейное преобразование φ конечномерного евклидова пространства Vn является симметрическим преобразованием тогда и только тогда, когда в Vn существует ортонормированный базис из собственных векторов φ (иначе говоря, СОН-базис преобразования φ).
Достаточность. Пусть в евклидовом пространстве Vn существует СОН-базис (е1,…,еn) (1) преобразования φ. Тогда φ(е1)=λ1е1; φ(е2)=0е1+ λ2е2;…; φ(еn)=0е1+…+ λnеn, так как еi – собственные векторы преобразования φ. Поэтому φ имеет в базисе (1) матрицу А=  . Так как А=А′, то А является симметрической матрицей. А это значит, в силу теоремы 2 из §4, что φ – симметрическое преобразование.
. Так как А=А′, то А является симметрической матрицей. А это значит, в силу теоремы 2 из §4, что φ – симметрическое преобразование.
Необходимость. Пусть φ – симметрическое преобразование n-мерного евклидова пространства Vn. Существование СОН-базиса будем доказывать индукцией по n.
1) n=1. Тогда V=<a>. Можно взять а=е1 – орт. Тогда V=<е1>. Так как φ (е1)  V, то φ(е1)=λ1е1 и е1 – собственный вектор φ. Значит, е1 – искомый СОН-базис.
V, то φ(е1)=λ1е1 и е1 – собственный вектор φ. Значит, е1 – искомый СОН-базис.
2) Пусть утверждение теоремы уже доказано для (n-1)-мерного евклидова пространства.
3) Докажем, что теорема верна для n-мерного евклидова пространства Vn. По следствию 2 теоремы 3 из §4 в Vn существует собственный вектор b преобразования φ, т.е. φ(b)=λ1b, λ1  R, b≠0. Нормируем его:
R, b≠0. Нормируем его:  =е1. Тогда φ(е1)=λ1е1; е1 – орт.
=е1. Тогда φ(е1)=λ1е1; е1 – орт.
Пусть Н=<е1>. Размерность Н равна 1. Если h  Н, то h= αе1. Так как φ(αе1)= αφ(е1)= αλ1е1
Н, то h= αе1. Так как φ(αе1)= αφ(е1)= αλ1е1  Н, то подпространство Н инвариантно относительно линейного преобразования φ.
Н, то подпространство Н инвариантно относительно линейного преобразования φ.
Рассмотрим Н┴. По теореме 2 из §6 главы 2 V=H  Н┴. Так как размерность Vn равна n, размерность Н равна 1, то из равенства dimVn = dimH + dimН┴ следует, что размерность Н┴ равна (n-1).
Н┴. Так как размерность Vn равна n, размерность Н равна 1, то из равенства dimVn = dimH + dimН┴ следует, что размерность Н┴ равна (n-1).
По теореме 1 из этого параграфа Н┴ инвариантно относительно φ, т.е. φ является и линейным преобразованием Н┴. Тогда φ – симметрическое преобразование (n-1)-мерного евклидова пространства Н┴. В силу предположения индукции в Н┴ существует СОН-базис е2,…,еn (1) преобразования φ.
Рассмотрим систему векторов е1, е2,…,еn (2). Здесь (е1, еi)=0 при любом i≠1, так как е1  Н, а еi
Н, а еi  Н┴. Далее, ej – орты и собственные векторы преобразования φ (j=1...n). Отсюда из ортонормированности системы (1) следует, что (2) – ортонормированная система из n векторов Vn. Так как эти векторы ненулевые, то она линейно независима, и потому (2) – искомый СОН-базис преобразования φ.
Н┴. Далее, ej – орты и собственные векторы преобразования φ (j=1...n). Отсюда из ортонормированности системы (1) следует, что (2) – ортонормированная система из n векторов Vn. Так как эти векторы ненулевые, то она линейно независима, и потому (2) – искомый СОН-базис преобразования φ.
Теорема доказана.
Следствие(матричная форма основной теоремы). Любая действительная симметрическая матрица А подобна некоторой диагональной матрице В, причем подобие можно осуществить с помощью ортогональной матрицы Q (т.е. Q-1AQ=B).
Доказательство. Пусть n – порядок матрицы А. Существует n-мерное линейное пространство над R (например, арифметическое R(n)). Если в нем задать скалярное произведение, то получим евклидово пространство Vn, размерность которого равна n.
Выберем в Vn некоторый ортонормированный базис е. Существует линейное преобразование φ пространства Vn, которое в базисе e имеет данную матрицу А. Так как А – симметрическая матрица, то по теореме 2 из §4 φ – симметрическое преобразование. По основной теореме (теорема 2) в Vn существует СОН-базис f преобразования φ. В нем φ имеет диагональную матрицу В. Следовательно, А и В – матрицы преобразования φ в разных ортонормированных базисах, а тогда эти матрицы подобны, т.е.
Q-1AQ=B, где Q – матрица перехода от е к f. Так как е и f – ортонормированные базисы, то Q по теореме 3 из §1 главы 2 – ортогональная матрица.
Следствие доказано.
§6. Приведение квадратичной формы к главным осям
Пусть f(x,x) – квадратичная форма с матрицей А, заданная на действительном линейном пространстве L, А – ее матрица. Как известно, матрица А симметрическая. По следствию из основной теоремы о симметрических преобразованиях (матричная форма основной теоремы) существует такая ортогональная матрица Q, что Q-1AQ=B (1), где В – диагональная матрица. Так как Q – ортогональная матрица, то Q-1=Q’. Из (1) следует, что B= Q’AQ (2). Мы знаем, что это равенство встречается в теории квадратичных форм: если квадратичную форму f с матрицей А подвергнуть невырожденному линейному преобразованию Х=QУ (3), то получим квадратичную форму с матрицей B= Q’AQ. Так как Q – ортогональная матрица, то (3) – ортогональное преобразование неизвестных. В силу (2), так как  , и после преобразования (3) f принимает вид: f=l1y12+...+lnyn2 (4). Это – канонический вид.
, и после преобразования (3) f принимает вид: f=l1y12+...+lnyn2 (4). Это – канонический вид.
Сформулируем и дополним полученный результат.
Теорема 3.Любую действительную квадратичную форму f(x,x) с помощью ортогонального преобразования неизвестных (3) можно привести к каноническому виду (4), причем этот вид единственный с точностью до обозначений неизвестных (такое приведение квадратичной формы называется приведением к главным осям.)
Доказательство. Существование доказано выше.
Единственность. Имеем: B = Q’AQ = Q-1AQ (так как Q – ортогональная матрица). Следовательно, матрица В подобна А. Так как характеристические многочлены подобных матриц совпадают, то  . Следовательно, l1…ln – спектр матрицы А, причем li ÎR. Но спектр матрицы единственен, и поэтому канонический вид (4) тоже единственен.
. Следовательно, l1…ln – спектр матрицы А, причем li ÎR. Но спектр матрицы единственен, и поэтому канонический вид (4) тоже единственен.
Теорема доказана.
Практическое приведение к главным осям
Пусть g(x,x) – действительная квадратичная форма, А – ее матрица. Пусть в евклидовом пространстве Vn найден СОН-базис симметрического преобразования j, имеющего в базисе е матрицу А (способ его нахождения смотрите ниже).
Если этим СОН-базисом будет f1,...,fn и Q – матрица перехода от е к f, то по доказанному выше Q’AQ=B, где В – диагональная матрица, по диагонали которой стоят характеристические корни  матрицы А. В СОН-базисе f квадратичная форма g(x,x) будет иметь канонический вид (4).
матрицы А. В СОН-базисе f квадратичная форма g(x,x) будет иметь канонический вид (4).
Практическое нахождение СОН-базиса
Для практического нахождения СОН-базиса φ поступаем так:
1) Находим все характеристические корни l1,..., ln (6) матрицы А, решая уравнение |А-lЕ|=0 (среди них могут быть и одинаковые). Они действительные, так как А – симметрическая матрица.
2) Записываем канонический вид g(x,x)= l1y12+...+lnyn2 . (7)
3) Пусть l1,..., ls – все различные характеристические корни матрицы А и ki – кратность характеристического корня li (i=1,...,s). Отметим, что
k1+…+ ks=n . (8)
Для дальнейшего нам понадобится лемма.
Лемма 1.Если l0 – характеристический корень кратности k0 симметрического преобразования φ конечномерного евклидова пространства Vn, то в Vn существует k0 линейно независимых собственных векторов, относящихся к собственному значению l0.
Доказательство. По основной теореме о симметрических преобразованиях в Vn существует СОН-базис f1,...,fn (9) преобразования φ. Матрица φ в этом базисе диагональная, причем по диагонали стоят числа (6). Среди этих чисел l0 встречается по условию k0 раз. Значит, в базисе (9) существует k0 собственных векторов преобразования φ, относящихся к собственному значению l0. Так как они линейно независимы (как часть базиса), то это искомые векторы.
Лемма доказана.
4)В силу леммы 1, решая систему уравнений (А- liЕ)Х=0,для каждого li (i=1,...,s) можно найти ki линейно независимых собственных векторов, относящихся к собственному значению li.
Ортогонализируем эту систему векторов с помощью процесса ортогонализации и нормируем каждый ее вектор.
Лемма 2.Собственные векторы симметрического преобразования φ, относящиеся к различным собственным значениям, ортогональны.
Доказательство. Пусть  ,
,  , причем
, причем  . Тогда
. Тогда  ,
,  . Так как φ – симметрическое преобразование, то
. Так как φ – симметрическое преобразование, то 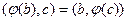 . Значит,
. Значит,  или, ввиду
или, ввиду  ,
,  .
.
Лемма доказана.
5)Соберем вместе все найденные выше системы векторов для i=1,2,...,s. Получим систему из n (в силу (8)) ортов. То, что эта система будет ортогональной, следует из леммы 2. Значит, мы получили искомый СОН-базис.
Если Q – матрица из координатных столбцов полученного СОН-базиса, то Х=QУ – ортогональное преобразование неизвестных, приводящее g(х,х) к каноническому виду (7).
Замечание.С помощью приведения квадратичной формы к главным осям можно находить канонический вид кривых и поверхностей 2-го порядка, приводя сначала к главным осям квадратичные формы из их уравнений.
ГЛАВА 4. АФФИННЫЕ ПРОСТРАНСТВА И АФФИННЫЕ ПРЕОБРАЗОВАНИЯ
§1. Определение аффинного пространства
В средней школе изучается геометрия плоскости и трехмерного пространства, основные объекты которой – точки и векторы. Наиболее полным и естественным алгебраическим обобщением этой геометрии является понятие аффинного пространства.
Определение 1.Пусть дано линейное пространство  над полем
над полем  и некоторое непустое множество А. Множество А называют аффинным, или точечно-векторным пространством, связанным с линейным пространством
и некоторое непустое множество А. Множество А называют аффинным, или точечно-векторным пространством, связанным с линейным пространством  , а его элементы точками аффинного пространства, если выполняются следующие аксиомы: 1) каждой упорядоченной паре точек
, а его элементы точками аффинного пространства, если выполняются следующие аксиомы: 1) каждой упорядоченной паре точек 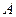 и
и 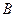 из множества А поставлен в соответствие единственный вектор
из множества А поставлен в соответствие единственный вектор 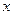 из линейного пространства
из линейного пространства  , обозначаемый так:
, обозначаемый так: 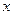
 ; 2) (аксиома откладывания) для каждой точки
; 2) (аксиома откладывания) для каждой точки 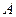
 А и каждого вектора
А и каждого вектора 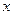

 существует единственная точка
существует единственная точка 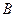
 А такая, что
А такая, что  (в этом случае будем писать:
(в этом случае будем писать:  , т.е.
, т.е. 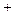 здесь символ того, что мы «откладываем» от точки
здесь символ того, что мы «откладываем» от точки 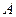 вектор
вектор 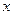 ); 3) для любых точек
); 3) для любых точек 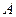 ,
, 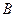 ,
, 
 А выполняется «правило треугольника»:
А выполняется «правило треугольника»:  .
.
Замечание.Линейное пространство  , с которым связано аффинное пространство А, называют пространством трансляций аффинного пространства А.
, с которым связано аффинное пространство А, называют пространством трансляций аффинного пространства А.
Из аксиом аффинного пространства получается рядследствий. Укажем только два из них:
1. Для любой точки 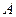
 А
А  . Действительно, для любой точки
. Действительно, для любой точки  В имеем:
В имеем:  . Поэтому
. Поэтому  – нулевой вектор.
– нулевой вектор.
2. . Из правила треугольника
. Из правила треугольника  , и потому
, и потому  .
.
Примеры аффинных пространств
1. Плоскость, прямая и трехмерное пространство из школьной геометрии.
2. Пусть  -поле, А
-поле, А  ={(
={( 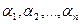 ,1)|
,1)|  },
}, 
 {(
{( 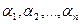 ,0)|
,0)|  }.Очевидно,
}.Очевидно,  . Элементы множества А
. Элементы множества А  назовем точками, а множества
назовем точками, а множества  – векторами. Если
– векторами. Если 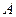 =(
=( 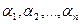 ,1),
,1), 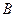 =(
=(  ,1) – две точки изА
,1) – две точки изА  , то полагаем
, то полагаем  .Нетрудно проверить выполнимость всех аксиом аффинного пространства. А
.Нетрудно проверить выполнимость всех аксиом аффинного пространства. А  называют
называют 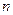 -мерным арифметическим аффинным пространством (над полем
-мерным арифметическим аффинным пространством (над полем  ).
).
§2. Система координат в аффинном пространстве
Определение 2. Векторы линейного пространства  называют свободными векторами аффинного пространства А. Если линейное пространство
называют свободными векторами аффинного пространства А. Если линейное пространство  является
является 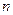 -мерным, то и аффинное пространство А называют
-мерным, то и аффинное пространство А называют 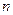 -мерным аффинным пространством.
-мерным аффинным пространством.
Определение 3.Системой координат, или репером, аффинного пространства А называют набор  (1), состоящий из точки
(1), состоящий из точки 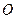
 А, называемой началом координат, и некоторого базиса
А, называемой началом координат, и некоторого базиса 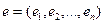 (2) линейного пространства
(2) линейного пространства  .
.
Определение 4. Координатами вектора 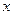 в репере (1) называют координаты этого вектора в базисе (2). Координаты вектора будем записывать в фигурных скобках:
в репере (1) называют координаты этого вектора в базисе (2). Координаты вектора будем записывать в фигурных скобках:  .
.
Определение 5. Координатами точки 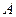
 А в репере (1) называют координаты вектора
А в репере (1) называют координаты вектора  (радиуса-вектора точки) в базисе (2).
(радиуса-вектора точки) в базисе (2).
Таким образом, координаты точки 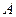 – это коэффициенты
– это коэффициенты 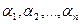 из выражения вектора
из выражения вектора  через базис
через базис  :
: 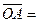
 =(
=( 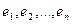 )
)  . Координаты точки будем записывать в круглых скобках:
. Координаты точки будем записывать в круглых скобках: 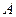 (
( 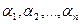 ).
).
Если  и
и  – две произвольные точки, то
– две произвольные точки, то  ,откуда
,откуда  . Так как
. Так как  ,
,  , то
, то  .
.
Как связаны координаты точек в разных реперах? Можно доказать (как в аналитической геометрии), что если
 ,
,  – координаты точки
– координаты точки 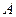 в двух реперах, тогда
в двух реперах, тогда 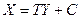 , где
, где  , а
, а  – матрицаперехода от старого базиса к новому.
– матрицаперехода от старого базиса к новому.
Замечание. Можно ввести понятие изоморфизма аффинных пространств.
Определение 6. Пусть дано взаимно однозначное отображение  множества всех точек и векторов аффинного пространства
множества всех точек и векторов аффинного пространства 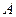 соответственно на множество всех точек и векторов аффинного пространства
соответственно на множество всех точек и векторов аффинного пространства 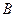 , которое является изоморфным отображением пространства трансляций аффинного пространства
, которое является изоморфным отображением пространства трансляций аффинного пространства 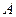 на пространство трансляций аффинного пространства
на пространство трансляций аффинного пространства 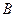 , и удовлетворяющее, кроме того, следующему условию: (v) если при отображении
, и удовлетворяющее, кроме того, следующему условию: (v) если при отображении  точки
точки  и
и  пространства
пространства 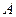 отображаются соответственно на точки
отображаются соответственно на точки  и
и  пространства
пространства 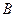 , то и вектор
, то и вектор 
 отображается на вектор
отображается на вектор 
 . Такое отображение называют изоморфным отображением аффинного пространства
. Такое отображение называют изоморфным отображением аффинного пространства 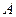 на аффинное пространство
на аффинное пространство 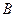 . Пространства
. Пространства 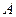 и
и 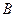 называют изоморфными между собой, если одно из них можно изоморфно отобразить на другое.
называют изоморфными между собой, если одно из них можно изоморфно отобразить на другое.
Так как изоморфизм между аффинными пространствами включает в себя изоморфизм их пространств трансляций, то, очевидно, всякие два изоморфных аффинных пространства имеют одну и ту же размерность.
Докажем, что и ноаборот, два аффинных пространства над одним полем, имеющие одну и ту же размерность, изоморфны между собой. Этот изоморфизм мы получим, построив изоморфное отображение произвольного 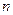 -мерного аффинного пространства
-мерного аффинного пространства  на арифметическое
на арифметическое 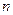 -мерное пространство
-мерное пространство 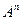 . Для этого возьмем в
. Для этого возьмем в  какой-нибудь репер
какой-нибудь репер  .Тогда каждая точка
.Тогда каждая точка  и каждый вектор
и каждый вектор 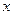 пространства
пространства  имеет единственные координаты в этом репере:
имеет единственные координаты в этом репере:
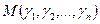 ,
,  .
.
Отображение  и
и  , очевидно, есть взаимно однозначное отображение множества всех точек и множества всех векторов пространства
, очевидно, есть взаимно однозначное отображение множества всех точек и множества всех векторов пространства  соответственно на множество всех точек и всех векторов пространства
соответственно на множество всех точек и всех векторов пространства 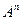 , удовлетворяющее, очевидно, условию (v). Изоморфизм между любым пространством
, удовлетворяющее, очевидно, условию (v). Изоморфизм между любым пространством  и пространством
и пространством 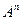 , а значит, и между любыми двумя
, а значит, и между любыми двумя 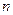 -мерными аффинными пространствами
-мерными аффинными пространствами 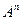 и
и  этим доказан.
этим доказан.
Мы доказали следующее утверждение (теорему 1).
Теорема 1.Два конечномерных аффинных пространства с пространством трансляций над одним полем тогда и только тогда изоморфны, когда они имеют одинаковые размерности.
§3. Плоскости в аффинных пространствах
Пусть задана некоторая система линейных уравнений с коэффициентами из поля  .
.
Определение 7. Будем говорить, что множество точек Д  А (или векторов из
А (или векторов из  ) удовлетворяет этой системе, если их координаты в некотором репере А (базисе
) удовлетворяет этой системе, если их координаты в некотором репере А (базисе  ) удовлетворяют этой системе.
) удовлетворяют этой системе.
Известно, что если дана некоторая неоднородная система линейных уравнений с 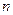 неизвестными и её приведенная однородная система, то
неизвестными и её приведенная однородная система, то
1) множество  всех решений этой однородной системы является подпространством
всех решений этой однородной системы является подпространством  линейного пространства
линейного пространства  ;
;
2) если  – частное решение неоднородной системы, то
– частное решение неоднородной системы, то  +
+  есть общее решение неоднородной системы.
есть общее решение неоднородной системы.
Если  , то
, то  можно считать координатами некоторой точки
можно считать координатами некоторой точки 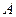 в репере
в репере 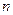 -мерного аффинного пространства А над полем
-мерного аффинного пространства А над полем  .
.
Мы видим, что данной неоднородной системе удовлетворяют все точки аффинного пространства А, записанные в виде 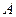 +
+  , где
, где 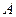
 А,
А,  – некоторое подпространство
– некоторое подпространство  , и только эти точки.
, и только эти точки.
Заметим, что если  – двумерное подпространство
– двумерное подпространство  , то
, то  +
+  – это плоскость в трехмерном пространстве.
– это плоскость в трехмерном пространстве.
В связи с этим естественно обобщить понятие плоскости для любого аффинного пространства.
Определение 8. Пусть А – аффинное пространство,  – некоторое подпространство
– некоторое подпространство  и dim
и dim  =
= 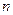 ,
,  . Множество
. Множество 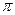 точек из А, для которых вектор
точек из А, для которых вектор  принадлежит
принадлежит  , т.е. множество, описываемое уравнением
, т.е. множество, описываемое уравнением
 , (3) где
, (3) где  ,
,  , называется
, называется  -мерной плоскостью.
-мерной плоскостью.
Точка  называется начальной точкой плоскости
называется начальной точкой плоскости 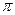 ,точка
,точка 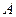 – текущей её точкой, подпространство
– текущей её точкой, подпространство  – направляющим подпространством этой плоскости.
– направляющим подпространством этой плоскости.
Из определения 8 видно, что  .
.
Можно показать, что всякая 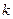 -мерная плоскость в аффинном пространстве А сама является аффинным пространством размерности
-мерная плоскость в аффинном пространстве А сама является аффинным пространством размерности 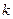 .
.
Отметим, что при 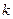 =0 (нульмерная плоскость) получается точка
=0 (нульмерная плоскость) получается точка  . Поэтому каждую точку аффинного пространства можно рассматривать как нульмерную плоскость. Само аффинное пространство является
. Поэтому каждую точку аффинного пространства можно рассматривать как нульмерную плоскость. Само аффинное пространство является 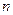 -мерной плоскостью. Одномерную плоскость называют прямой, (
-мерной плоскостью. Одномерную плоскость называют прямой, ( 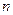 -1)-мерную плоскость – гиперплоскостью. В трехмерном пространстве это будет, как нетрудно видеть, плоскость.
-1)-мерную плоскость – гиперплоскостью. В трехмерном пространстве это будет, как нетрудно видеть, плоскость.
В определение плоскости введена её начальная точка. Можно показать, что в качестве начальной точки плоскости можно взять любую её точку. Из этого следует, что две плоскости, имеющие одну общую точку и одно и то же направляющее подпространство, совпадают.
Пусть в аффинном пространстве А выбрана система координат  , где
, где  А,
А, 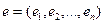 – базис линейного пространства свободных векторов, и дана
– базис линейного пространства свободных векторов, и дана 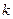 -мерная плоскость
-мерная плоскость  , проходящая через точку
, проходящая через точку  с направляющим подпространством
с направляющим подпространством  (где
(где  – базис
– базис  ).
).
Тогда  ,
,  и рассматриваемую плоскость можно записать в виде
и рассматриваемую плоскость можно записать в виде
 , (4)
, (4)
где  – параметры, принимающие произвольные числовые значения из поля
– параметры, принимающие произвольные числовые значения из поля  независимо друг от друга.
независимо друг от друга.
Определение 9. Уравнение (2) называют параметрическим уравнением рассматриваемой плоскости в векторной форме.
Пусть в выбранной системе координат

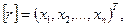
 .
.
Тогда, переходя от векторного равенства  к покоординатным равенствам, получим систему уравнений
к покоординатным равенствам, получим систему уравнений
 (5)
(5)
Определение 10. Систему (5) называют параметрическими уравнениями 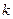 -мерной плоскости, проходящей через точку
-мерной плоскости, проходящей через точку  в направлении пространства
в направлении пространства  .
.
В частном случае 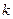 =1
=1 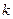 -мерная плоскость есть прямая. При этом подпространство
-мерная плоскость есть прямая. При этом подпространство  порождается одним вектором
порождается одним вектором  с координатами
с координатами  , а параметрические уравнения прямой (4) принимают вид
, а параметрические уравнения прямой (4) принимают вид
 (6)
(6)
При 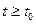 на прямой (6) выделяется луч, а при
на прямой (6) выделяется луч, а при  – отрезок.
– отрезок.
От параметрических уравнений прямой (6) легко перейти к ее каноническим уравнениям
 . (7)
. (7)
Исключив из параметрических уравнений (5) 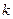 -мерной плоскости все параметры, получим ее общие уравнения
-мерной плоскости все параметры, получим ее общие уравнения
 (8)
(8)
В частности, гиперплоскость, соответствующая случаю  , задается одним уравнением
, задается одним уравнением
 .
.
В системе уравнений (8) каждое отдельное можно рассматривать как уравнение гиперплоскости, а всю систему уравнений – как определение 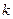 -мерной плоскости пересечением
-мерной плоскости пересечением 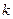 гиперплоскостей. Это наглядно иллюстрируется на примере прямых в трехмерном пространстве, так как любая такая прямая может рассматриваться как пересечение двух плоскостей.
гиперплоскостей. Это наглядно иллюстрируется на примере прямых в трехмерном пространстве, так как любая такая прямая может рассматриваться как пересечение двух плоскостей.
Получив уравнение прямых и плоскостей в аффинном пространстве, можно решать все вопросы аналитической геометрии относительно прямых и плоскостей в этом пространстве, точнее вопросы относительно прямых и плоскостей, не связанные с измерением длин и углов. В частности, здесь можно развить теорию выпуклых множеств и выпуклых многогранников, нужную для линейного программирования.
Определение 11. Будем говорить, что некоторая система линейных уравнений с 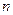 неизвестными с коэффициентами из
неизвестными с коэффициентами из  задает плоскость
задает плоскость 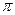 , если этой системе удовлетворяют координаты всех точек из
, если этой системе удовлетворяют координаты всех точек из 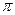 в некотором репере, и только они.
в некотором репере, и только они.
Из сказанного следует, что справедлива следующая теорема.
Теорема 2. Совместная система линейных уравнений с 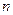 неизвестными над полем
неизвестными над полем  задает некоторую
задает некоторую  -мерную плоскость в аффинном пространстве А, причем
-мерную плоскость в аффинном пространстве А, причем  =
=  , где
, где  – ранг системы.
– ранг системы.
Замечание. Из теоремы 2 следует, что в трехмерном аффинном пространстве всякая система линейных уравнений ранга 1 задает плоскость, а ранга 2 – прямую.
Справедливо утверждение, обратное теореме 2.
Теорема 3. Любая  -мерная плоскость
-мерная плоскость 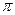
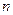 -го аффинного пространства А с направляющим подпространством
-го аффинного пространства А с направляющим подпространством  может быть задана системой (
может быть задана системой (  ) линейно независимых уравнений.
) линейно независимых уравнений.
Доказательство. Известно, что любое  -мерное подпространство
-мерное подпространство 
 -мерного линейного пространства
-мерного линейного пространства  над
над  может быть задано однородной системой (
может быть задано однородной системой (  ) линейно независимых уравнений
) линейно независимых уравнений  (9)
(9)  (т.е. координаты
(т.е. координаты  любого вектора из
любого вектора из  в некотором базисе и только этих векторов удовлетворяют этой системе уравнений). По определению плоскости, если
в некотором базисе и только этих векторов удовлетворяют этой системе уравнений). По определению плоскости, если  – начальная точка плоскости
– начальная точка плоскости  , то
, то  тогда и только тогда, когда
тогда и только тогда, когда ⇐ Предыдущая44454647484950515253Следующая ⇒