Главная | Обратная связь

Изоморфизм евклидовых пространств

 

Определение 5. Два евклидовых пространства V и V’ называются изоморфными, если существует биекция φ: V→V’, удовлетворяющая условиям:

1) φ – изоморфизм линейных пространств V и V’;

2) при отображении φ сохраняется скалярное произведение, т.е. (φ(a), φ(b))=(a, b) для любых a, b Î V.

Такое отображение φ называется изоморфным отображением или изоморфизмом евклидовых пространств V и V’.

Теорема (критерий изоморфизма конечномерных евклидовых пространств). Два конечномерных евклидовых пространства V и V’ изоморфны тогда и только тогда, когда dimV=dimV’ (10).

Необходимость. Пусть V V’. Тогда по определению 5 они изоморфны, как линейные пространства, и, как известно, выполняется (10).

Достаточность. Пусть dimV=dimV’=n (11). Выберем в V ортонормированный базис e₁,…,e_n (12), в V’ –ортонормированный базис e’₁,…,e’_n (13). Возьмем любой вектор а из V: . Определим отображение φ так: полагаем (15). Нетрудно проверить, что φ – изоморфизм линейных пространств V и V’.

Покажем, что при отображении φ сохраняется скалярное произведение.

Пусть (16). По определению φ имеем: (17). Так как базис (12) ортонормированный, то по теореме 4 (18). Но базис (13) также ортонормированный, и поэтому (19). Из (18) и (19) получаем: .

Значит, φ – изоморфизм евклидовых пространств V и V’, т.е. V V’.

Теорема доказана.

Следствие.Если конечномерное действительное линейное пространство L любыми способами превращается в евклидово пространство, то получаются изоморфные евклидовы пространства (так как их размерность одна и та же и равна dim L).

Этим мы ответили на вопрос 1 из замечания 2 §1 этой главы.

§6. Ортогональные дополнения подпространств

Определение.Множество Н┴ всех векторов евклидова пространства V, ортогональных к каждому вектору его подпространства Н, называют ортогональным дополнением к Н.

Пример. В евклидовом пространстве векторов-отрезков на плоскости ОХ┴=ОУ.

Теорема 1.Ортогональное дополнение Н┴ к подпространству Н евклидова пространства V является подпространством V.

Доказательство. Пусть у₁,у₂ Н┴. Тогда для любого вектора х Н имеем: (х, у₁)=0 и (х, у₂)=0. Следовательно, (х, у₁+у₂)= (х, у₁)+(х, у₂)=0, т.е. вектор у₁+у₂ ортогонален любому вектору х Н. Это означает, что (у₁+у₂) Н┴. Мы доказали, что сумма любых двух векторов множества Н┴ принадлежит Н┴. Аналогично для любого действительного числа λ и любого х Н имеем:

(х, λ у₁)= λ(х, у₁)= λ∙0= 0, т.е. вектор λу₁ ортогонален любому вектору х Н, а значит, принадлежит Н┴. Таким образом, множество Н┴ замкнуто относительно сложения векторов и умножения векторов на числа и, следовательно, является подпространством евклидова пространства V.

Теорема доказана.

Теорема 2.Пусть V – конечномерное евклидово пространство, Н – его подпространство. Тогда справедливо равенство: V=Н Н┴.

Доказательство. Рассмотрим Н∩Н┴. Пусть (Н∩Н┴) h. Тогда (h,h)=0, и поэтому h=0 и Н∩Н┴=0.

Докажем, что V=Н+Н┴. В Н выберем ортогональный базис h₁,…,h_s (он существует, так как Н – конечномерное евклидово пространство). Его можно дополнить до базиса V. Пусть h₁,…,h_s, h_s+1,…,h_n (1) – такой базис. Если к (1) применить процесс ортогонализации, начиная с вектора h_s+1, то из (1) получится ортогональный базис V: h₁,…,h_s, b_s+1,…,b_n. Имеем: H = < h₁,…,h_s > (2). Рассмотрим подпространство S=< b_s+1,…,b_n > (3). Очевидно, что S Н┴, так как любой вектор h Н представим в виде и , ибо . Далее . Отсюда, учитывая (2) и (3), следует, что а (Н+S).

Следовательно, V= Н+S, а так как S Н┴, то V=Н+Н┴. Но (Н∩Н┴)=0, и поэтому V=Н Н┴.

Теорема доказана.

§7. Унитарные пространства

Для случая линейных пространств над полем С комплексных чисел понятие скалярного произведения несколько видоизменяется, точнее, изменяется аксиома 1 и частично аксиома 4.

Определение 6.Будем говорить, что в линейном пространстве L над полем С определено скалярное произведение, если любой упорядоченной паре a, b L поставлено в соответствие единственное комплексное число (a, b) и выполняются следующие требования для любых a, b, с 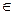L и любого a 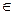C:

1) ;

2) (a+b, c)=(a,c)+(b,c);

3) (aa,b)=(a,b);

4) (a,a) ÎR и (a,a)>0 при а 0.

Определение 7. Линейное пространство над С, в котором задано скалярное произведение, удовлетворяющее условиям 1) –4), называется унитарным пространством.

Для большинства результатов, полученных в теории евклидовых пространств, можно получить близкие к ним утверждения и для унитарных пространств. В частности, отметим, что и в ортонормированных базисах унитарного пространства скалярное произведение вычисляется по такой формуле: .

С основными результатами, полученными в теории унитарных пространств, можно ознакомиться, например, по книгам [5] и [3].