Главная | Обратная связь

ГЛАВА 6. МНОГОЧЛЕНЫ ОТ НЕСКОЛЬКИХ НЕИЗВЕСТНЫХ

§1. Кольцо многочленов от n неизвестных

Определение 1.Многочленом f(x₁,x₂,…,x_n) от n неизвестных x₁,x₂,…,x_n над некоторым полем Р называется сумма конечного числа членов вида , где все k_i≥0 и аÎР.

Лемма 1.Пусть К – кольцо без делителей нуля, и f(x), g(x) – два многочлена из К[x]\0. Тогда deg f(x)g(x)=deg f(x) + deg g(x).

Доказательство. Пусть f(x)=a₀xⁿ+…+a_n, g(x)=b₀x^m+…+b_m, a₀≠0, b₀≠0 (1). Тогда f(x)g(x)= a₀b₀xⁿ+…+a_nb_m (2). Так как в К нет делителей нуля, то из неравенств (1) следует, что a₀ b₀≠0, а тогда из (2) получаем deg f(x)g(x)=m+n= deg f(x) + deg g(x).

Лемма доказана.

Следствие.При условиях леммы в К[x] нет делителей нуля (ибо из f(x) ≠0 и g(x)≠0 и леммы 1 следует, что f(x)g(x)≠0).

Лемма 2.Пусть К – кольцо без делителей нуля, тогда множество К[x] – кольцо без делителей нуля.

Доказательство. То, что К[x] – кольцо, доказывается так же, как и ранее для Р[х], где Р – произвольное поле.

Отсутствие в К[x] делителей нуля доказано в следствии леммы 1.

Лемма доказана.

Теорема 1.Множество P[x₁,x₂,…,x_n] всех многочленов от n неизвестных над полем Р– кольцо без делителей нуля.

Доказательство. Доказательство будем проводить индукцией по n. Действительно, при n=1 утверждение верно в силу леммы 2. Пусть уже доказано, что множество P[x₁,x₂,…,x_n-1]=S многочленов от n-1 неизвестных x₁,x₂,…,x_n-1 с коэффициентами из поля Р составляют кольцо без делителей нуля.

Всякий многочлен f(x₁,…x_n) от n неизвестных x₁, x₂,…,x_n-1, x_n можно представить, притом единственным способом, как многочлен от неизвестного x_n с коэффициентами, являющимися многочленами от x₁,x₂,…,x_n-1, т.е. из кольца S: P[x₁,x₂,…,x_n]=S[x_n]. И наоборот, всякий многочлен от x_n с коэффициентами из кольца S можно рассматривать, конечно, как многочлен над полем Р от всей совокупности неизвестных x₁, x₂,…,x_n-1, x_n. Значит, P[x₁,x₂,…,x_n]=S[x_n]. (3)

По лемме 2 S[x_n] – кольцо без делителей нуля. Теперь из (3) следует, что P[x₁,x₂,…,x_n] – кольцо без делителей нуля.

Теорема доказана.

Определение 2.Степенью члена называется число m=k₁+…+k_n.

Для многочленов от одного неизвестного мы имеем два естественных способа расположения членов – по убывающим и по возрастающим степеням неизвестного. В случае многочленов от нескольких неизвестных такие способы уже отсутствуют. Например, если дан многочлен, все члены которого имеют пятую степень – f(х₁,х₂,х₃)= х₁х²₂х²₃+ х⁴₁х₃+х³₂х²₃+х²₁х₂х²₃, – то его можно записать и в виде f(х₁,х₂,х₃)= х⁴₁х₃ +х²₁х₂х²₃ +х₁х²₂х²₃+ +х³₂х²₃, и нет оснований одну из этих записей предпочесть другой.

Существует, однако, способ вполне определенного расположения членов многочлена от нескольких неизвестных, зависящий, впрочем, от выбора нумерации неизвестных; для многочленов от одного неизвестного он приводит к расположению членов по убывающим степеням неизвестного.

Этот способ, называемый лексикографическим, подсказан обычным приемом расположения слов в словарях: считая буквы упорядоченными так, как это принято в алфавите, мы определяем взаимное положение двух данных слов в словаре по их первым буквам, если же эти буквы совпадают, то по вторым буквам и т.д.

Если теперь «алфавитом» считать {x₁,x₂,…,x_n}, то по указанному выше способу можно сравнить два любых члена многочлена.

Пусть (4) и (5) – два (неподобных) члена многочлена f(x₁,…x_n).

Определение 3. Будем говорить, что член (4) выше члена (5), если k₁>t₁ или k₁=t₁, но k₂>t₂, и т.д. (обратите внимание, что коэффициенты a и b при таком сравнении не принимаются во внимание).

Теперь можно расположить члены многочлена «по высоте»: первый – член, который выше всех остальных, за ним – член, который выше всех из оставшихся и т.д. Такое расположение членов многочлена называется лексикографическим.

Пример. Так, члены многочлена f(x₁,x₂,x₃,x₄)=x₁⁴+3x₁²x₂³x₃–x₁²x₂³x₄²+5x₁x₃x₄² +2x₂+x₃³x₄–4 расположены лексикографически.

Определение 4.Член многочленаf(x₁,x₂,…,x_n), который выше всех других его членов, называется высшим членом этого многочлена.

Нетрудно доказывается следующая лемма.

Лемма 3.Высший член произведения двух или нескольких многочленов от n неизвестных равен произведению высших членов сомножителей.

Доказательство этого утверждения можно посмотреть в [1].

§2. Симметрические многочлены

Определение 5. Многочлен f(х₁,…,х_n)ÎP[х₁,…,х_n] называется симметрическим многочленом, если он не меняется при любой перестановке неизвестных.

Чтобы проверить, является ли данный многочлен симметрическим, достаточно убедиться, что он не меняется при перестановке любых двух входящих в него неизвестных, т.е. при их транспозиции, ибо любая перестановка неизвестных х₁,…,х_n может быть получена путем последовательного выполнения конечного числа транспозиций.

Среди симметрических многочленов от n неизвестных особую роль играют суммы всевозможных произведений по 1,2,...,n:

. (1)

Их называют элементарными симметрическими многочленами.

Нетрудно видеть, что множество всех симметрических многочленов с коэффициентами из поля Р составляет кольцо, так как сумма и произведение симметрических многочленов, очевидно, являются симметрическими многочленами. Его называют кольцом симметрических многочленов.

Лемма 4.Пусть 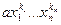– высший член симметрического многочлена f(х₁,…,х_n). Тогда выполняются неравенства k₁³...³k_n.

Доказательство. Предположим противное. Тогда существуют число i такое, что k_i+1>k_i (2). Высший член многочлена f(х₁,…,х_n) запишем подробнее: 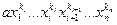(3). В многочлене f(х₁,…,х_n) поменяем местами неизвестные х_i и x_i+1, а остальные неизвестные оставим на своих местах. Тогда его высший член перейдет (ввиду того, что f – симметрический многочлен) в следующий член этого многочлена: 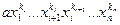= 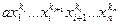. В силу неравенства (2) этот член выше высшего члена (3), что противоречит определению высшего члена.

Следовательно, k_i+1£ k_i для любого i=1,…,n-1. Лемма доказана.

Теорема(основная теорема о симметрических многочленах).Всякий симметрический многочлен от неизвестных х₁,…,х_n с коэффициентами из поля Р можно представить в виде многочлена от элементарных симметрических многочленов s₁,… s_n c коэффициентами, принадлежащими этому же полю.

Доказательство. Пусть 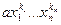– высший член симметрического многочлена f(х₁,…,х_n). В силу леммы 4 выполняются неравенства k₁³...³k_n (4). Составим следующее выражение: (5).

В силу (4) k_i - k_i+1³0, поэтому ₁ – многочлен от s₁,…, s_n. Если в многочлен ₁ вместо s_i подставить их выражения через х₁,…,х_n, то получится некоторый многочлен от х₁,…,х_n. Так как высший член произведения равен произведению высших членов сомножителей и высший член s₁ равен х₁, s₂ – х₁х_2, … s_n – х₁...x_n, то из (5) следует, что высшим членом многочлена j₁ будет = = .

Высший член многочлена ₁ оказался таким же, что и высший член многочлена f. Поэтому разность f- ₁=f₁ будет симметрическим многочленом от х₁,…,х_n, у которого высший член ниже высшего члена f.

Возможны два случая:

1) f₁=0. Тогда f- ₁=0. Следовательно, f= ₁(s₁ ,…, s_n ) и теорема доказана.

2) f₁¹0. Тогда точно так же по высшему члену f₁ составляется многочлен ₂(s₁ ,…, s_n), такой, что разность f₁- ₂=f₂= f₁- ₁- ₂ будет симметрическим многочленом, у которого высший член ниже высшего члена f₁, и, следовательно, ниже высшего члена f, и т.д.

Покажем, что через конечное число шагов f_s=0. Тогда f_s= f- ₁- ₂-…- _s=0, т.е. f= ₁+ ₂+…+ _sÎP[s₁,…, s_n], и теорема будет доказана. Для этого рассмотрим высший член (6) любого промежуточного многочлена f_j(х₁,…,х_n). Так как f_j – симметрический многочлен, то по лемме 4 имеем: l₁³...³l_n (7). Но высший член f_j ниже высшего члена f, и потому l₁£ k₁. Отсюда и из (7) следует, что l_i£ k₁ (8) для любого i=1,…,n.

Нетрудно видеть, что наборов l₁,...,l_n с условиями (7) и (8), где l_iÎNÈ0, существует лишь конечное число. Значит, описанная выше процедура через конечное число шагов закончится.

Теорема доказана.

Замечание1. Другими словами, основная теорема означает: любой симметрический многочлен f(х₁,…,х_n)ÎP[х₁,…,х_n] можно выразить через элементарные симметрические многочлены с помощью операций сложения, умножения и умножения на элементы поля Р.

Замечание2.Можно доказать, что выражение симметрического многочлена через элементарные симметрические многочлены единственно.

§3. Однородные симметрические многочлены

Определение 6. Многочлен от n неизвестных называется однородным степени m, если все его члены имеют одну и ту же степень m.

Нетрудно видеть, что любой многочлен можно представить в виде суммы однородных многочленов, поэтому, чтобы научиться выражать симметрический многочлен через элементарные симметрические многочлены, достаточно уметь это делать для однородных симметрических многочленов.

Пусть f – однородный симметрический многочлен с высшим членом , k₁+k₂+…+k_n= m. Тогда f – однородный многочлен степени m. Нетрудно видеть, что многочлены f_j, появляющиеся при доказательстве основной теоремы, тоже будут однородными многочленами степени m, так как _i – однородные многочлены степени m. Это значит, что в (7) l₁+l₂+…+l_n=m.

Учитывая это, можно сформулировать следующий алгоритм для выражения однородного симметрического многочлена f через элементарные симметрические многочлены:

1) выписываем высший член 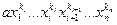многочлена f;

2) находим сумму k₁+k₂+…+k_n=m;

3) из высшего члена f выписываем набор показателей k₁,k_2,…,k_n;

4) составляем всевозможные наборы l₁,l₂,…,l_n, l_jÎNÈ0, 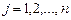, удовлетворяющее условиям:

а) l₁³...³l_n (для того, чтобы член мог быть высшим членом промежуточного симметрического многочлена f_j);

б) l₁£ k₁, чтобы член был ниже члена ;

в) l₁+l₂+…+l_n=m.

Для каждого найденного выше набора l₁,...,l_n составляем многочлен вида , где c_i – неизвестное число. Затем записываем f в виде суммы полученных многочленов f=φ₁+φ₂+ φ_s (8), где s – число составленных в п. 4) наборов. Коэффициенты c_i находим из системы уравнений, которая получится, если придавать неизвестным х₁,…,х_n определенные наборы значений.

Замечание.Описанным выше методом неопределенных коэффициентов можно пользоваться ввиду единственности выражения симметрического многочлена через элементарные симметрические многочлены.

Часто приходится решать рассмотренную в этом параграфе задачу для частного вида однородных многочленов – моногенных многочленов.

Определение 6. Симметрический многочлен от неизвестных х₁,…,х_n , все члены которого могут быть получены из высшего члена путем всевозможных перестановок неизвестных, называется моногенным многочленом.

Если 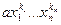- высший член моногенного многочлена, то этот многочлен обозначается через S( 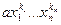) или

Примеры. х₁х₂+ х₁х₃+ х₂х₃, х₁^k+ х₂^k+… х_n^k (степенная сумма).

 

§4. Значение симметрического многочлена от корней уравнения

Пусть задано уравнение вида a₀xⁿ+a₁x^n-1+…+a_n-1x+a_n=0 (9);где a₀ ≠0, , Р – поле, и симметрический многочлен f(х₁,…,х_n). Требуется найти f(х₁⁰,…,х_n⁰), где {х₁⁰,…,х_n⁰} – все корни данного уравнения.

Эту задачу можно решать так:

1) Получим из данного уравнения приведенное уравнение (разделив его на а₀):

xⁿ+b₁x^n-1+…+b_n-1x+b_n=0.

Очевидно, что корни этого уравнения те же, что и у данного (9).

2) Используем теорему Виета:

х₁⁰+…+х_n⁰= -b₁,

х₁⁰х₂⁰+…+х_n-1⁰х_n⁰= b₂,

. . . . . . . . . . . . . . . . .

х₁⁰…х_n⁰= (-1)ⁿb_n.

Если ввести обозначения _i⁰= _i(х₁⁰,…,х_n⁰), i=1,...,n, то эти равенства перепишутся так:

₁⁰=-b₁,

₂⁰= b₂, (10)

. . . . . . . . .

_n⁰= (-1)ⁿb_n.

Мы нашли значения ₁⁰ ,… _n⁰ элементарных симметрических многочленов от корней данного уравнения.

3) Симметрический многочлен f выразим через элементарные симметрические многочлены: f(х₁,…,х_n)= (s₁ ,…, s_n ). Если сюда подставить корни уравнения (9) и учесть (10), то получим f(х₁⁰,…,х_n⁰)= (s₁⁰,…,s_n⁰)= (-b₁,b₂,…,(-1)ⁿb_n).

Задача решена.

Таким, образом, не находя корней уравнения n-ой степени от одного неизвестного (что обычно невозможно сделать при n³5), мы можем вычислить значение любого симметрического многочлена от этих корней.