 |
|
Глава 3. Уравнения для электрических цепей в переходном состоянии
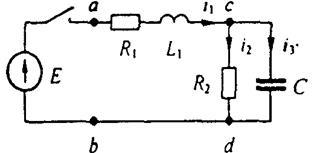 3.1. Составление уравнений для свободных токов и напряжений. Для послекоммутационной схемы составляют уравнения по законам Кирхгофа для полных токов и напряжений, так же как это делалось и раньше: сначала обозначают токи в ветвях и произвольно выбирают для них положительные направления, затем составляют уравнения по первому и второму законам Кирхгофа. Так, для схемы рис. 6 после выбора положительных направлений для токов имеем
3.1. Составление уравнений для свободных токов и напряжений. Для послекоммутационной схемы составляют уравнения по законам Кирхгофа для полных токов и напряжений, так же как это делалось и раньше: сначала обозначают токи в ветвях и произвольно выбирают для них положительные направления, затем составляют уравнения по первому и второму законам Кирхгофа. Так, для схемы рис. 6 после выбора положительных направлений для токов имеем
i1+ i2+ i3=0
L(di1 /dt)+R1 i1+R2 i2=Е
R2 i2 – ( 1/С)∫ i3dt = 0 ( 18 )
Рис.6
В этих уравнениях i1, i2 , i3 — полные токи. Каждый из них состоит из свободного и принужденного токов. Для того чтобы от этой системы уравнений перейти к уравнениям для свободных токов, "освободим" систему от вынуждающих ЭДС (в нашем случае от ЭДС Е) и вместо i1, запишем i1св, вместо i2— i2св и т. д. В результате получим:
i1св+ i2св+ i3св=0
L(di1св /dt)+R1 i1св+R2 i2св=Е
R2 i2св – ( 1/С)∫ i3свdt = 0 ( 19 )
Заметим, что для любого контура любой электрической цепи сумма падений напряжений от свободных составляющих токов равна нулю.
3.2. Алгебраизация системы уравнений для свободных токов.
В 1.3 говорилось о том, что свободный ток представляет собой решение однородного дифференциального уравнения (уравнения без правой части). Как известно из курса математики, решение однородного дифференциального уравнения записывают в виде показательных функций например, в виде суммы экспонент
Хсв(t) = А1• е р t + А2• е рt+ А3 • е рt+… ( 20 )
где А1, А2, А3, ... - постоянные интегрирования
Р1, Р2. ,Р3 - корни характеристического уравнения.
Таким образом, уравнение для каждого свободного тока можно представить в виде
iсв = А• е рt ( 21 )
Постоянная интегрирования А для каждого свободного тока своя. Показатели же затухания р одинаковы для свободных токов ветвей. Физически это объясняется тем, что вся цепь охвачена единым (общим) переходным процессом.
Составим производную от свободного тока:
(diсв /dt) = [d(А• е рt)]dt = p А• е рt = piсв ( 22 )
Следовательно, производную от свободного тока можно заменить на piсв, а свободное напряжение на индуктивном элементе L(di1св /dt) на Lр·iсв .
Найдем интеграл от свободного тока:
∫ iсвdt = ∫ А е рt dt = (А е рt)/р =iсв / р ( 23 )
Постоянная интегрирования взята здесь равной нулю, так как свободные составляющие не содержат не зависящих от времени слагаемых. Следовательно, интеграл от свободного тока можно заменить на iсв/р а свободное напряжение на конденсаторе (1/С) ∫ iсвdt — на ( iсв/рС).
В систему дифференциальных уравнений для свободных токов под
ставим L piсв. вместо L(diсв /dt) и ( iсв/рС).вместо (1/С)∫ iсвdt . Следовательно,
i1св+ i2св+ i3св=0
(L1р+R1) i1св+R2 i2св=0 ( 24 )
R2 i2св – ( i3св/рС) = 0
Уравнения (24) представляют собой систему алгебраических уравнений относительно i1св; i2св; i3св и, в отличие от исходной системы, не содержат производных и интегралов.
Переход от системы линейных дифференциальных уравнений к
системе алгебраических уравнений называют алгебраизацией системы
дифференциальных уравнений для свободных токов. Можно сказать, что
система (24) есть результат алгебраизации системы дифференциальных
уравнений (19).