Главная | Обратная связь

Определение степени характеристического уравнения.

Степень характеристического уравнения цепи необходимо уметь оценивать,взглянув на схему, в которой исследуется переходный процесс. Быстрая ориентация позволяет определить трудоемкость предстоящих выкладок и способствует выявлению ошибки, если она возникает при составлении характеристического уравнения.

Степень характеристического уравнения равна числу основных неза­висимых начальных значений в послекоммутационной схеме после мак­симального ее упрощения и не зависит от вида ЭДС источников ЭДС в схеме.

Упомянутое упрощение состоит в том, что последовательно соединен­ные индуктивные элементы должны быть заменены одним эквивалент­ным; конденсаторы, включенные последовательно и параллельно, тоже должны быть заменены эквивалентными.

Применительно к схеме на рис.7, а последовательно включенные L^'₁ и L"₂ следует заменить на L = L^'₁ + L"₂ ±2 M, если между ними есть маг­нитная связь (если нет магнитной связи, то М =0), а конденсаторы ем-

Рис.7

остью C^'₃, C^''₃, C₄— на конденсатор емкостью С₅ = С₄ + [ (C^'₃ ·C^''₃ ) / (C^'₃ + C^''₃) ]

Начальное значение напряжения на С₅ равно начальному значению на­пряжения на С₄.

В результате упрощений схемы рис.7, а получаем схему рис.7, б, в которой два индуктивных элемента и один конденсатор. Все три неза­висимых начальных значения — основные. Следовательно, характерис­тическое уравнение будет третьей степени.

Обратим внимание на то, что степень характеристического уравнения не зависит от того, имеется ли магнитная связь между индуктивными элементами схемы или она отсутствует.

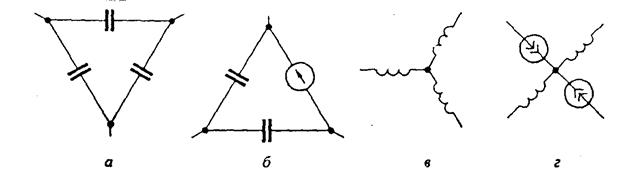Условимся под емкостным контуром понимать контур, в каждой из ветвей которого имеются либо только конденсаторы (рис. 8, а), либо в одни ветви входят только конденсаторы, а в другие — только источники ЭДС (рис. 8, 6). Положим, что после максимального упрощения схемы

в емкостный контур входит n конденсаторов. Если учесть, что по второ­му закону Кирхгофа алгебраическая сумма напряжений на ветвях конту­ра равна нулю, то только на n-1 конденсаторах контура напряжения могут быть заданы произвольно. Условимся под индуктивным узлом по­нимать узел, в котором сходятся ветви, в каждой из которой имеются индуктивности (рис.8, в), либо часть ветвей с индуктивностями, а дру­гая с источниками тока (рис.8, г). Положим, что в индуктивный узел сходится m-ветвей, содержащих индуктивности. Если учесть, что по пер­вому закону Кирхгофа сумма токов в узле равна нулю, то только в m - 1 индуктивностях токи могут быть заданы произвольно.

Обобщенно можно сказать, что после максимального упрощения схемы степень характеристического уравнения может быть определена путем подсчета величины n_L + n_c –у_L -к_c , где n_L— число индуктив­ных элементов в схеме; n_c - число конденсаторов; у_L — число индук­тивных элементов, токи в которых не могут быть заданы произвольно; к_c -— число конденсаторов, напряжения на которых не могут быть зада­ны произвольно.

Замечания. I. Если схема с источником тока имеет несколько последовательных участков, содержащих параллельно соединенные ветви с R, L, С, то для каждой группы параллельных ветвей будет свое характеристическое уравнение со своими корнями (сво­бодные токи не могут замыкаться через источник тока, поскольку его сопротивление рав­но бесконечности).

2. Если в схеме будут иметься так называемые дополняющие двухполюсники , содержащие элементы R, L, С, между которыми выполняются определенные соотношения, то при упрощении схемы они должны быть заменены на эквивалентные им резисторы. Это значительно упрощает выкладки .