 |
|
Проекція вектора на вісь. Основна теорема про проекцію
Нехай задано вектор 
і напрямлена вісь 
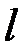. Опустимо перпендику-
ляри з точок 
і 
на пряму 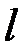. Проекції точок і на пряму 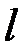позначимо відповідно 
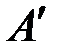і 
. Отримаємо вектор 
.
Означення.Проекцією вектора 
на вісь 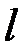називається довжина вектора 
, яку взято зі знаком « 
», якщо напрям вектора збігається з напрямом осі 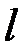(рис. 9), та зі знаком « 
» у протилежному випадку (рис.10).
Рис. 9
Рис.10
Позначається проекція вектора на вісь 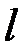так: 
.
Таким чином:
(рис. 9).
(рис.10).
Теорема.Проекція вектора на вісь 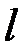дорівнює довжині вектора , яку помножено на косинус кута 
між вектором і напрямом осі .
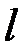Доведення.Розглянемо спочатку ситуацію, яка відповідає рис. 9. Очевидно, що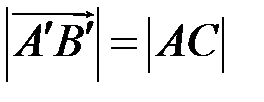 
, а з прямокутного трикутника 
випливає, що
,
і теорему у цьому випадку доведено. Розглянемо ситуацію, що відповідає рис. 10. Тоді:
,
і теорему доведено повністю.
Сформулюємо основні властивості проекцій.
1. 
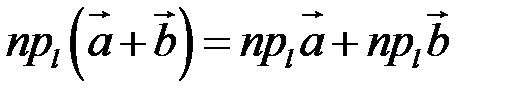, тобто проекція суми векторів на вісь дорівнює
сумі проекцій векторів на цю вісь (рис. 11).
Рис. 11
2. 
, де 
– число.
Дійсно, позначимо як 
кут між вектором 
і віссю 
, а як 
– кут між вектором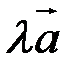 
і віссю . Тоді, якщо 
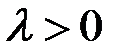, то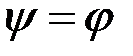 
, і матимемо:
.
Якщо 
, то 
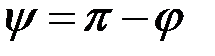, і матимемо:
Тобто лінійні дії над векторами переходять у відповідні лінійні дії над проекціями.
4. Компланарні та некомпланарні вектори. Базис у просторі
Означення.Вектори називаються компланарними, якщо вони лежать у одній площині, або в паралельних площинах (рис. 12).
З означення випливає, що будь які два вектори завжди будуть компланарними, адже два вектори завжди лежать в паралельних площинах.
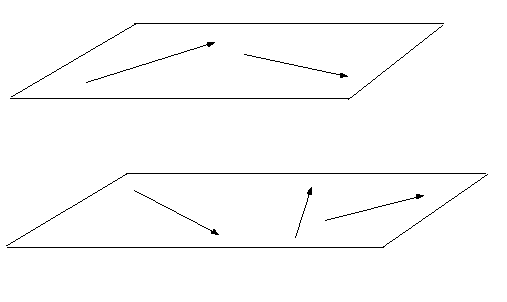
Рис. 12
Таким чином, щоб вектори були некомпланарними, їх має бути принаймні три (рис. 13).
Рис. 13
Означення.Базисом у просторі називається довільна упорядкована трійка некомпланарних векторів.
З означення випливає, що ці вектори мають бути ненульовими, адже у протилежному випадку вони були б компланарними.
Зауваження. Базис можна ввести також на прямій та на площині. Базисом на прямій називається довільний ненульовий вектор. Базисом на площині називається довільна упорядкована пара ненульових неколінеарних векторів.
Теорема (про розкладання вектора за базисом). Нехай вектори 
утворюють базис у просторі. Тоді для будь якого вектора 
простору існує єдина трійка чисел 
, що справджується рівність:
.
Доведення. Зведемо вектори 
до одного початку і побудуємо на векторах 
паралелепіпед так, щоб вектор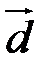 
був його діагоналлю (рис. 14).
Рис. 14
Вектори, що відповідають ребрам паралелепіпеда, позначимо через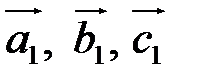 
, а вектор, що відповідає діагоналі паралелепіпеда, позначимо 
.
Оскільки вектор 
колінеарний вектору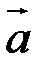 
, то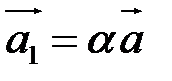 
, відповідно 
. Очевидно, що 
, 
, що й треба було довести.
Числа 
називаються координатами вектора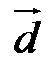 
в базисі 
.
Введемо поняття орієнтованих трійок векторів.
Означення. Упорядкована трійка некомпланарних векторів називається правою (рис. 15а), якщо з кінця вектора 
найкоротший поворот від вектора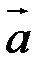 
до вектора 
видно проти годинникової стрілки. Якщо цей поворот видно за годинниковою стрілкою (рис. 15б), то трійка називається лівою.
Рис. 15а Рис. 15б
Назви трійок мають таке походження. Великий, вказівний та середній пальці правої руки (перераховані саму у такому порядку) утворюють праву трійку, а ті ж самі пальці, перераховані у такому ж самому порядку, лівої руки утворюють ліву трійку.
Означення. Стандартним базисом у просторі називається права трійка взаємно перпендикулярних одиничних векторів 
(рис. 16), які називаються ортами.
Рис. 16
Такий базис ще називається ортонормованим. Згідно з вище доведеною теоремою для будь якого вектора 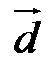існує єдина трійка чисел 
(координат вектора 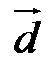), що буде виконана рівність:
.