 |
|
Задачі до розділу 6
1. Двовимірна випадкова величина задана функцією розподілу:
.
Визначити ймовірність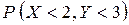 
.
Відповідь: 9/16.
2. Двовимірна випадкова величина задана функцією розподілу:
.
Визначити ймовірність попадання випадкової точки (x, y) в прямокутник (2 < Х < 3; 3 < Y < 4).
Відповідь: 
3. Двовимірна випадкова величина задана функцією розподілу:
, 
.
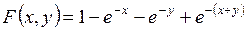Визначити щільність розподілу 
.
Відповідь: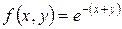 
.
4. Задано закон розподілу двовимірної випадкової величини (X,Y):
| X/Y | 1,00 | 3,00 | 3,50 | 4,00 |
| 1,50 | 0,20 | 0,00 | 0,00 | 0,00 |
| 2,00 | 0,10 | 0,15 | 0,00 | 0,00 |
| 3,00 | 0,00 | 0,03 | 0,18 | 0,04 |
| 4,00 | 0,00 | 0,00 | 0,10 | 0,20 |
Обчислити кореляційний момент і коефіцієнт кореляції величин X та Y, визначити, чи є вони залежними (незалежними)?
Відповідь: 
0,995; 
; X та Y пов’язані сильною лінійною залежністю.
5. Задано закон розподілу двовимірної випадкової величини (X,Y):
 Y
X
| 2,30 | 4,00 | 9,70 | 16,00 |
| 1,50 | 0,20 | 0,00 | 0,00 | 0,06 |
| 2,00 | 0,00 | 0,15 | 0,10 | 0,00 |
| 3,00 | 0,00 | 0,0 | 0,18 | 0,11 |
| 4,00 | 0,10 | 0,00 | 0,10 | 0,00 |
Обчислити кореляційний момент і коефіцієнт кореляції величин X та Y, визначити, чи є вони залежними (незалежними)?
Відповідь: 0,88, 
; між X та Y існує слабка лінійна залежність (або можлива нелінійна залежність).
6. Дано кореляційну матрицю системи двох нормально розподілених випадкових величин (X, Y) 
. Знайти диференціальну функцію розподілу ймовірностей f(x, y) і її максимальне значення, якщо відомі математичні сподівання компонентів: Mx = 3, My = 0 .
Розв’язування
На головній діагоналі кореляційної матриці розташовані дисперсії компонентів: Di = kii. Тому 
Крім того, кореляційний момент 
. Знайдемо коефіцієнт кореляції:
.
Диференціальна функція f(x, y) має такий вигляд:
Оскільки показник степені у виразі для функції f(x, y) не може бути додатним, то максимального значення функція буде набувати, коли він дорівнює нулю, тобто коли 
. За цих умов значення функції:
.
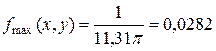Відповідь: 
7. Визначити ймовірність попадання двовимірної випадкової величини (X,Y) у заштриховану область (рис 6.6), якщо інтегральна функція розподілу ймовірностей F(x,y)відома.
Рис. 6.6. Область попадання ВВ (до задачі 7)
Розв’язування
Імовірність попадання ВВ(X, Y) у заштриховану область дорівнює різниці площ прямокутників S1 і S2 (рис. 6.6), тобто
.
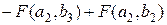8. Визначити диференціальну функцію розподілу ймовірностей, математичні сподівання й кореляційну матрицю системи випадкових величин (X, Y) заданих в інтервалах 
й 
, якщо інтегральна функція цієї системи 
.
Розв’язування
Диференціальна функція дорівнює другій змішаній похідній від інтегральної функції, тобто
.
Математичне сподівання випадкової величини Х розраховується у такий спосіб:
Очевидно, що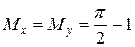 
.
Дисперсії розраховуються таким чином: 
Інтегруючи двічі за частинами, одержимо: 
. Крім того, 
.
Визначимо кореляційний момент у такий спосіб:
Отже, кореляційна матриця системи (X, Y) має такий вигляд:
.
9. Диференціальну функцію системи випадкових величин (X, Y) визначено такою формулою: 
.
Знайти сталу А і записати інтегральну функцію.
Відповідь: 
.
10. Знайти диференціальну функцію розподілу ймовірностей системи двох випадкових величин (X, Y) відповідно до її інтегральної функції: 
, 
.
Відповідь: 
.
11. Визначити ймовірність попадання двовимірної випадкової величини (X, Y) у заштриховану область (рис. 6.7), якщо відома інтегральна функція F(x,y).
Рис. 6.7. Область попадання ВВ (до задачі 11)
Відповідь: 
.
12. Визначити ймовірність попадання двовимірної випадкової величини (X,Y) в область, описану такими нерівностями: 
, коли відома інтегральна функція:
тут 
.
Відповідь: 
.
13. Система випадкових величин (X, Y) підпорядковується закону рівної ймовірності усередині прямокутника із абсцисами (0; а) і ординатами (0; b). Визначити ймовірність попадання випадкової величини (X, Y) у коло радіуса R, якщо a > b > R , а координати центра кола (0, 0).
Відповідь: 
.
14. Дано закон розподілу двовимірної дискретної ВВ(X, Y). Знайти коефіцієнт кореляції rxy.
| X Y | |||
| 0,05 | 0,15 | 0,35 | |
| 0,3 | 0,1 | 0,05 |
Відповідь: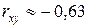 
.
15. Визначити щільність імовірності системи двох нормально розподілених випадкових величин, для яких 
й 
, коли x = 2; y = 2.
Відповідь: 0,00563.
Частина 2