Главная | Обратная связь

Статистичний розподіл вибірки

 

Нехай потрібно вивчити сукупність об’єктів відносно деякої кількісної або якісної ознаки.

Інколи з цією метою проводять загальне обстеження, тобто вивчають кожен об’єкт сукупності. Але часто провести таке обстеження фізично неможливо (наприклад, сукупність складається з дуже великої кількості об’єктів) або не має практичного сенсу (якщо обстеження об’єкта пов’язується із його фізичним знищенням чи потребує великих матеріальних витрат). У таких випадках довільно відбирають із усієї сукупності обмежену кількість об’єктів, вивчають їх і на підставі отриманих результатів роблять висновки про властивості всієї сукупності об’єктів.

Генеральною сукупністю називають сукупність об’єктів, яку необхідно вивчити.

Вибірковою сукупністю, або просто вибіркою, називають сукупність об’єктів, відібраних довільно з генеральної сукупності для обстеження.

Вибірки можуть бути повторними та безповторними.

Повторною називається вибірка, у якій відібраний об’єкт (перед вибором наступного) повертається в генеральну сукупність.

Безповторною називають вибірку, в якій відібраний об’єкт у генеральну сукупність не повертається.

Для того, щоб за результатами обстеження об’єктів вибірки можна було робити висновки про об’єкти генеральної сукупності або про їхні властивості, необхідно, щоб об’єкти вибірки правильно їх відображали. Це можна сформулювати так: вибірка повинна бути репрезентативною, тобто найбільш характерною для об’єкта дослідження.

Нехай із генеральної сукупності взято вибірку із n об’єктів. Число n називається обсягом вибірки. Позначимо через x₁, x₂, …, x_n кількісні величини вимірюваної ознаки об’єкта. Припустимо, що значення x₁ спостерігалося n₁ разів, x₂ – n₂ разів, x_k – n_k разів. Значення х_і , які спостерігаються, називаються варіантами, а послідовність варіант, яка записана у порядку збільшення – варіаційним рядом. Число спостережень варіанти х_і називають частотами іпозначають n_i, а відношення їх до обсягу вибірки – відносними частотами, тобто . Сума всіх частот дорівнює обсягу вибірки:

,

сума відносних частот дорівнює одиниці:

.

Статистичним розподілом вибірки називають перелік варіант і відповідних їм частот або відносних частот.

 

Статистичний розподіл можна записати у вигляді таблиці таким чином:

 

xi	x1	x2	x3	…	xk
ni	n1	n2	n3	…	nk

 

тут x_i – варіанти, n_i – відповідні їм частоти.

 

П р и к л а д 7.1. Нехай унаслідок спостереження одержано вибірку:

1, 2, 2, 2, 1, 3, 3, 4, 5, 4, 3, 1, 2, 5, 4, 4, 3, 5, 2, 4, 1, 2, 1, 5, 5.

Записати статистичний розподіл вибірки у частотах і відносних частотах.

Розв’язування

Вибірка містить 25 елементів. Тож обсяг вибірки n = 25.

Задамо розподіл частот вибірки у вигляді таблиці. У її верхньому рядку записуємо варіанти, а в нижньому – відповідні їм частоти. У нашому випадку маємо такі варіанти: 1, 2, 3, 4, 5. Значення 1 трапляється у вибірці 5 разів, тому його частота дорівнює 5. Аналогічно визначаємо частоти інших варіант і остаточно маємо такий розподіл:

 

xi
ni

 

Обчислимо для перевірки суму частот: . Сума дорівнює обсягу вибірки, отже, розподіл складено правильно.

Визначимо розподіл відносних частот. Знайдемо відносні частоти за формулою: . Результати обчислень запишемо у вигляді таблиці.

xi
Wi	0,2	0,24	0,16	0,2	0,2

 

Зауважимо, що коли вибірку отримують із значень неперервної випадкової величини, такий спосіб не завжди буває зручним, бо може виявитися, що вибірка містить багато даних, різниця між якими незначна і які характеризуються малими частотами. Тоді статистичний розподіл записують у вигляді послідовності інтервалів і відповідних їм частот. За частоту інтервалу беруть суму частот варіант, що містяться в цьому інтервалі.

У загальному випадку інтервальний розподіл має такий вигляд:

 

xi	(α0, α1)	(α1, α2)	(α2, α3)	...	(αk-1, αk)
ni	n1	n2	n3	…	nk

 

Він може бути записаний також і у відносних частотах.

Крім табличних, існують графічні засоби подання статистичного розподілу. До них відносяться полігон і гістограма.

Полігоном частот називають ламану лінію, відрізки якої з’єднують точки (x₁,n₁), (x₂,n₂) … (x_k,n_k).

Полігоном відносних частот називають ламану лінію, відрізки якої з’єднують точки (x₁,W₁), (x₂,W₂) … (x_k,W_k).

П р и к л а д 7.2. Побудувати полігон частот статистичного розподілу, який подано таблицею:

 

xi
ni

Розв’язування

Для побудови полігону на осі абсцис відкладемо варіанти х_і, а на осі ординат – відповідні їм частоти (рис. 7.1).

 

Рис. 7.1. Полігон частот статистичного розподілу з прикладу 7.2

 

Якщо вимірюються значення неперервної випадкової величини, то доцільно будувати гістограму. Для цього інтервал, у якому перебувають усі значення, поділяють на декілька часткових інтервалів довжиною h_і, і для кожного з них обчислюють суму частот варіант, які в ньому перебувають.

Гістограмою частот називають східчасту фігуру, що складається із прямокутників, основи яких відповідають частковим інтервалам, а висоти дорівнюють відношенню (щільність частоти).

Обчислимо площу і-го часткового прямокутника: . Вочевидь, вона дорівнює сумі частот варіант і-го інтервалу і відповідно площа гістограми частот дорівнює обсягу вибірки.

Гістограмою відносних частот називають східчасту фігуру, яка складається з прямокутників, основи яких являють собою часткові інтервали довжиною h_і, а висоти дорівнюють відношенню .

Площа гістограми відносних частот дорівнює одиниці.

Гістограма відносних частот використовується для оцінки диференціальної функції розподілу ймовірності.

П р и к л а д 7.3. Побудувати гістограму відносних частот для даного статистичного розподілу.

 

xi	(1;3)	(3; 5)	(5; 7)	(7; 9)	(9, 12)
ni

 

Розв’язування

Запишемо розподіл у відносних частотах. Обсяг вибірки за нашими даними

 

xi	(1;3)	(3; 5)	(5; 7)	(7; 9)	(9, 12)
Wi	0,32	0,26	0,2	0,16	0,06

 

Обчислимо висоту кожного з прямокутників гістограми, а саме:

 

, , ,

, .

 

Користуючись розрахованими даними, будуємо гістограму (рис. 7.2).

 

Рис. 7.2. Гістограма відносних частот за статистичним розподілом з прикладу 7.3

 

 

Емпіричною функцією розподілу (функцією розподілу вибірки) називають функцію , яка для кожного значення аргументу х дорівнює відносній частоті події Х < x, тобто

,

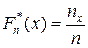де n_x – число варіант, менших за х, n – обсяг вибірки.

 

Якщо обсяг вибірки n великий – емпірична функція розподілу прямує до теоретичної. Це підтверджується також і тим, що має ті самі властивості, що й F(x), а саме:

1. Значення належать відрізку [0,1].

2. , якщо х₁ х₂.

3. Якщо х_min – найменша варіанта, то , коли х х_min;

якщо x_max – найбільша варіанта, то , коли x > x_max.

 

Емпірична функція розподілу використовується для оцінки теоретичної функції розподілу генеральної сукупності.