Главная | Обратная связь

Залежні та незалежні випадкові величини

Випадкова величина У називається незалежною від випадкової величини Х, якщо закон розподілу величини У не залежить від того, яке значення прийняла величина Х.

Для неперервних випадкових величин умова незалежності У від Х має вигляд при будь-якому у. Якщо ж У залежить від Х, то

(1)

Доведемо, що залежність або незалежність випадкових величин завжди взаємні: якщо величина У не залежить від Х, то і величина Х не залежить від У.

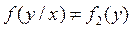
Дійсно, нехай У не залежить від Х:

Тоді і (1) Доведено.

Іще одне означення: Випадкові величини Х і У називаються незалежними, якщо закон розподілу кожної із них не залежить від того, яке значення прийняла друга. В іншому випадку величини Х і У називаються залежними. Для незалежних випадкових величин теорема множення законів розподілу: (2), тобто щільність розподілу системи незалежних випадкових величин дорівнює добутку щільностей розподілу окремих величин, які входять с систему. Умова (2) є необхідна та достатня умова незалежності випадкових величин.

Приклад. Щільність розподілу систему (X,Y) має вигляд:

Визначити, чи залежні, чи незалежні випадкові величини X та Y.

Із того, що функція розпалась на добуток функцій, із яких одна залежить тільки від x, інша – тільки від y, випливає, що X і Y – незалежні. Дійсно:

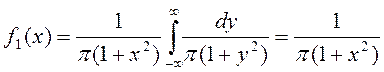
За аналогією . Звідки X та Y є незалежні.

Лекція 3

Числові характеристик системи двох випадкових величин. Кореляційний момент. Коефіцієнт корекції

Початковим моментом порядку K, S системи (X,Y) називають математичне сподівання добутку на

(1)

Центральним моментом порядку K, S системи (X,Y) називають математичне сподівання добутку та степеня відповідних центрованих величин

(2)

(3)

(4)

Де , а сума поширюється на всі можливі значення випадкових величин X, Y.

Для неперервних випадкових величин:

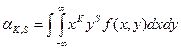(5)

(6)

Математичні сподівання:

та представляють собою характеристику положення системи. Геометрично це координати середньої точки на площині, навколо якої відбувається розсіяння точки (X,Y).

Дисперсії:

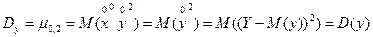
Вони характеризують розсіяння випадкової точки в напрямку вісі OX та OY. Другий змішаний центральний момент:

Він грає дуже велике значення:

(7)

Характеристика називається кореляційним моментом випадкових величин X та Y.

Для дискретних випадкових величин X і Y:

(8)

а для неперервних:

(9)

Кореляційний момент є характеристика системи випадкових величин, яка описує зв'язок між ними. Для того, щоб переконатись в цьому, доведемо, що для незалежних випадкових величин кореляційний момент дорівнює нулю.

Нехай X, Y – незалежні неперервні випадкові величини з щільністю f(x,y):

, (10)

де , – відповідний щільності розподілу випадкових величин X і Y.

Таким чином, якщо кореляційний момент двох випадкових величин , то це є ознака наявності залежності між ними.

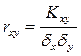(11)

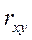– коефіцієнт кореляції. для незалежних випадкових величин дорівнює нулю.

характеризує не тільки тісноту зв’язку, але й розсіяння. Якщо X дуже мало відрізняється від , а Y знаходиться в сильній залежності від X, то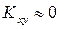

Для цього і вводять .

Випадкові величини, для яких =0, називаються некорельованими.

Але поняття некорельованості не є еквівалентним поняттю незалежності. Із незалежності випливає некорельованість. А навпаки? Відповідь – ні!

Приклад. Розглянемо систему випадкових величин (X, Y), розподілену з рівномірною щільністю всередині круга С радіуса r з центром в початку координат.

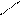
y

С₂ С₁ r

С₃ С₄ x

С

Із умови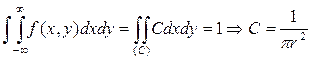

Не важко переконатись, що величини є залежними. Дійсно, якщо X прийме значення, наприклад, 0, то Y з рівною ймовірністю може прийняти всі значення від –r до +r; якщо ж X=r, то Y тільки прийме одне значення Y=0. Взагалі, діапазон можливих значень Y залежить від того, яке значення прийме X.

Із-за умови симетрії

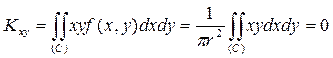
В секторах С₁, С₃ підінтегральна функція додатня, С₂, С₄ – від’ємна; за абсолютним значенням ці інтеграли рівні.

Таким чином, із некорельованості випадкових величин не завжди слідує їх незалежність.

Коефіцієнт кореляції характеризує не будь-яку залежність, а тільки лінійну залежність (при зростанні або при спаданні однієї випадкової величини інша теж зростає або спадає, але лінійно). Коефіцієнт кореляції характеризує степінь тісноти лінійної залежності між випадковими величинами. Якщо Y=aX+b, (точна лінійна залежність), то (+1, якщо а>0; –1, якщо a<0)

В загальному випадку: .У випадку кажуть про додатню кореляцію величин X та Y; – від’ємна кореляція.

Додатня кореляція: при зростанні однієї випадкової величини – інша теж зростає; в другому випадку спадає.

В розглянутому прикладі лінійна залежність відсутня; при зростанні X змінюється тільки діапазон зміни Y, а його середнє значення не змінюється; природньо, що величини (X,Y) є некорельованими.

Лекція №4