Побудова таблиць циліндрів

Основними задачами приведеного тут аналізу є: класифікація схем циліндрів, математичний розрахунок матриці зв’язності по заданих параметрах циліндра та побудова на цій основі таблиць циліндрів.

Будь-які два циліндри з однаковими матрицями зв’язності назвемо еквівалентними та суворо еквівалентними, якщо вони до того ж мають однаковий склад навантажувальних групп, що підключаються до кожної лінії.

Параметр двохкрокового циліндра (рис. 7.4 а) позначимо i . Перша навантажувальна группа має зв’язок з (i+1)-ю та (g+1-i)-ю групами. Якщо ввести додатковий параметр z=g-i, то зв’язки первшої групи будуть i+1 і z+1. Очевидно, що циліндри з параметрами (i)_z та (z)_i суворо еквівалентні.

Параметри трьохкрокового (рис. 7.4 б) позначимо через i та j 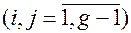. Зв’язки першої групи з урахуванням порядка підключення навантажувальних груп наступні:

, , .

При введенні додаткового параметра z=g-i-j в запису зв’язків простежується чітка закономірність:

, , .

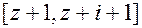Таким чином, при циклічному зсуві параметрів циліндра (i,j)_z матриця зв’язності і склад підключених навантажувальних груп не міняються. Отже, циліндри з параметрами (i,j)_z, (j,z)_i і (z,i)_j суворо еквівалентні. Якщо змінити порядок параметрів на зворотній, то матриця зв’язності залишиться попередньою, але зміниться склад підключених груп: , , 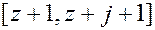. Отримані нові циліндри (z,j)_i, (i,z)_j, (i,j)_z суворо еквівалентні між собою, але по відношенню до початкових просто еквівалентні.

Наступну групу еквівалентних циліндрів утворюють реверсивні схеми, які можна отримати з будь-якої попередньої, змінивши порядок рахунку навантажувальних груп на зворотній або примінивши формули перерахунку параметрів:

, , ,

де i₁, j₁, z₁ – параметри вихідної схеми, i₂, j₂, z₂ – параметри реверсивної схеми.

Реверсивні циліндри по відношенню до вихідних є просто еквівалентними. Однак, у реверсивних циліндрів, отриманих зі схем типу (i,j)_z, буде такий же склад підключених навантажувальних груп, як у циліндрів типу (z,j)_i, і навпаки. Таким чином, можна утворити 12 еквівалентних трьохкрокових циліндрів: дві групи по 6 суворо еквівалентних між собою циліндрів. Наприклад, при g=7 на основі циліндра (1,2)₄ можна побудувати наступні еквівалентні схеми:

1. (1,2)₄, (2,4)₁, (4,1)₂;

2. (4,2)₁, (2,1)₄, (1,4)₂;

3. (6,5)₃, (5,3)₆, (3,6)₅;

4. (3,5)₆, (5,6)₃, (6,3)₅.

Перша і третя групи циліндрів мають наступний склад підключених груп: 1,2,4; 1,3,7; 1,5,6; друга і четверта – 1,3,4; 1,2,6; 1,5,7. Матриця зв’язності в обох випадках однакова: перша група має по одному зв’язку з усіма іншими групами, однак поєднання підключених груп різні.

Для чотирьохкрокового циліндра з параметрами (i,j,k)_z, 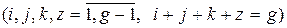зв’язки першої групи такі:

, ,

, .

По аналогії з попереднім суворо еквівалентни такі схеми, отримані циклічним зсувом параметрів: (i,j,k)_z, (j,k,z)_I, (k,z,i)_j і (z,i,j)_k. Наступну групу суворо еквівалентних між собою циліндрів можна отримати, надавши параметрам зворотнього порядку: (z,k,j)_i, (i,z,k)_j, (j,i,z)_k, (k,j,i)_z. Реверсивні схеми циліндрів також аналогічні попередньому.

В загальному випадку кожна навантажувальна група d-крокового циліндра має зв’язків з іншими групами. Номера груп, з котрими пов’язана перша група, легко визначити, виходячи з параметрів циліндра та приведених вище формул. З будь-якого циліндра, використовуючи циклічний зсув параметрів, можна отримати d (з урахуванням вихідної) суворо еквівалентних схем. Розташувавши параметри в зворотньому порядку, визначимо другу групу з d суворо еквівалентних схем. Між собою ці групи будуть просто еквівалентні. По формулах реверсивних циліндрів отримаємо ще дві групи по d суворо еквиівалентних схем. Якщо деякі параметри співпадають, число еквівалентних циліндрів відповідно скорочується.

Базуючись на приведених співвідношеннях, отримані таблиці трьох-, чотирьох-, п’яти-, шестикрокових нееквівалентних циліндрів (табл. 7.1 і 7.2). З усіх можливих варіантів схем відібрані ті, що дозволяють швидко отримати оптимальні НВ. В таблицях вказані зв’язки тільки з першою половиною груп, бо друга половина є дзеркальним відображенням: групі 1+а завжди відповідає група g+1-a. Так, для циліндра (1,3)повний рядок при g=10 має вид 3101101101, при g=11 – 31011001101.

Таблиця 7.1

Трьохкрокові схеми нееквівалентних циліндрів

Число груп	Параметри схеми	Число зв’язків першої навантажу-вальної групи з групою	Рекомендована послідовність схем

1	2	3	4	5	6	7	8	9	10
	(1,2)								(1,2)
	(1,1) (1,2)								(1,2) (1,2)
	(1,1) (1,2) (2,2)								(1,2) (1,1) (1,2) (1,2) (1,1) (2,2) (1,2) (1,2) (1,1) (1,2)
	(1,2)								(1,2)
	(1,2) (1,3) (2,2)								(1,2) (1,3) (1,2) (2,2) (1,2) (1,3) (1,2)
	(1,2) (1,3) (1,4) (2,3)								(1,2) (1,4) (2,3) (1,2)
	(1,2) (1,3) (1,4) (2,2) (2,3)								(1,2) (1,4) (1,3) (2,2) (2,3) (1,3)
	(1,2) (1,3) (1,4) (2,3) (2,4)								(1,2) (1,4) (2,3) (1,3) (2,4)
	(1,2) (1,3) (1,4) (1,5) (2,3) (2,4) (3,4)								(1,2) (1,4) (2,4) (2,3) (1,3) (1,5) (2,3) (1,3) (2,4) (2,3) (1,4)
	(1,2) (1,3) (1,4) (1,5) (2,3) (2,4) (2,5) (3,4)								(1,3) (2,5)
	(1,2) (1,3) (1,4) (1,5) (1,6) (2,3) (2,4) (2,5) (3,4) (3,5)								(1,3) (2,5) (2,4) (1,5) (3,5) (1,2) (3,4) (1,4) (2,4) (2,3) (1,6)
	(1,2) (1,3) (1,4) (1,5) (1,6) (2,3) (2,4) (2,5) (2,6) (3,4) (3,5) (4,5)								(1,3) (2,5) (2,4) (1,5) (3,5) (1,3) (2,6)

Таблица 7.2

Чотирьохкрокові схеми нееквівалентних циліндрів

Число груп	Параметри схеми	Число зв’язків першої навантажу-вальної групи з групою	Рекомендована послідовність схем

	(1,1,2)			(1,1,2)
	(1,1,1) (1,1,2) (1,2,1)			(1,1,1) (1,1,2) (1,2,1) (1,1,1) (1,1,2)
	(1,1,2)			(1,1,2)
	(1,1,2) (1,1,3) (1,2,2) (1,2,3)			(1,1,2) (1,1,3) (1,2,2) (1,1,2) (1,2,3) (1,1,3) (1,1,2)
	(1,1,2) (1,1,3) (1,2,1) (1,2,2) (1,2,4) (1,3,2)			(1,1,2) (1,3,2) (1,1,3) (1,2,4) (1,2,1) (1,2,3)
	(1,1,2) (1,1,3) (1,2,1) (1,2,2) (1,2,3) (1,2,4) (1,3,2)			(1,1,2) (1,2,3) (1,3,2) (1,1,3) (1,2,4) (1,2,2) (1,2,2) (1,2,1) (1,3,2)
	(1,1,3) (1,2,2) (1,2,4) (1,2,5) (1,3,2)			(1,2,3) (1,2,2) (1,2,4) (1,2,5) (1,3,2)
	(1,1,3) (1,2,2) (1,2,4) (1,2,5) (1,3,5)			(1,2,4) (1,1,3) (1,2,4) (1,2,2) (1,2,4) (1,2,5) (1,2,4) (1,3,5) (1,2,4) (1,2,2)
	(1,3,5)			(1,3,2)
	(1,2,4) (1,2,5) (1,2,7) (1,3,2) (1,4,2) (1,4,3) (2,4,3)			(1,3,2) (2,4,3) (1,3,2) (1,4,3) (1,3,2) (1,4,2) (1,3,2) (1,2,5) (1,3,2) (1,2,4) (1,3,2) (1,2,7) (1,3,2)
	(1,2,4) (1,2,7) (1,2,8) (1,3,2) (1,3,5) (1,4,2) (2,3,4)			(2,3,4) (1,3,5) (1,4,2) (1,2,7) (1,2,4) (1,2,8) (1,3,2)

⇐ Предыдущая 26 27 28 29 303132 33 34 35 Следующая ⇒