Главная | Обратная связь

Аналітичний метод розрахунку НВ

Розглядається математична модель типу М/М/v,G/L. На схему НВ загального вигляду надходить найпростіший потік викликів з параметром Λ. Припускається, що число входів n в кожній групі настільки велике порівняно з D, що не впливає на властивості вхідного потоку. Тоді при i < D переходи в системі здійснюються аналогічно повнодоступній схемі (п.5.1). Перехід же зі стану i = D в стан i = D+1 можливий тільки в тому випадку, якщо виклик надходить від джерела навантажувальної групи, в якій є вільною хоча б одна з D доступних ліній. Якщо ж виклик надійде від джерела навантажувальної групи, в якій зайняті всі D доступних ліній, він буде втрачений. Щоб урахувати можливу недоступність вільних ліній, введемо функцію φ_i, рівну умовній імовірності встановлення з’єднання для виклика, що надійшов у стані i, тобто коли зайнято ліній. Очевидно, φ_i=1при , φ_i<1 при и φ_v=0. Запишемо систему рівнянь для усталеного режиму:

(7.8)

Вирішуючи (7.8), отримуємо:

(7.9)

Отриманий вираз називають третім розподілом Ерланга. При φ_k=1 для всіх з (7.9) випливає перший розподіл Ерланга. Оскільки для найпростішего потоку викликів усі три види втрат рівні між собою, обмежимося визначенням імовірності Р_в. У стані i імовірність втрати виклика , отже,

. (7.10)

Інтенсивність обслугованого навантаження

(7.11)

Значення функції φ_i легко визначається для т.з. ерланговських ідеально симетричних схем (ІСС). Ідеально симетричним називають таке рівномірне НВ, при якому кожній навантажувальній групі доступна своя, відмінна від інших комбінація з D ліній, а загальне число груп дорівнює числу таких комбінацій . При симетричному вхідному навантаженню і рівноімовірнім зайнятті вільних ліній імовірність зайняття будь-якої конкретної комбінації в ІСС однакова и не залежить від виду комбінації. При зайнятості в ІСС ліній 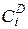навантажувальних груп із загального числа будуть заблоковані. Отже, імовірність блокування

(7.12)

На рис. 7.5 зображена ІСС при D=2, v=4 і g=C₄²=6. Під кожною групою вказана відповідна комбінація доступних ліній. Добре видно, що при зайнятості будь-яких двох ліній завжди буде заблокована одна група. Оскільки на всі групи надходить навантаження з однаковою інтенсивністю та імовірність будь-якої комбінації зайнятих ліній однакова, то 1- φ₂=1/6. При зайнятості трьох будь-яких ліній завжди будуть заблоковані три групи. Наприклад, зайнятим лініям 1, 2 и 4 відповідають заблоковані групи 1, 4 и 5. Отже 1-φ₃=3/6.

Практичного використання ІСС не отримали, бо для їх побудови навіть при D=10 потрібно завелике число навантажувальних груп. Однак, результати їх розрахунку приміняються для оцінки втрат в реальних НВ. Серед рівномірних схем ІСС є найкращими, але вже при γ≥3,0 більшість рівномірних НВ дуже близькі за пропускною здатністю до ІСС. В області малих втрат (менш 0,01) і при послідовному зайнятті оптимальні ступеневі НВ можуть перевищувати ІСС за пропускною здатністю.

Для реальних схем НВ функция φ_i має вигляд

. (7.13)

Коефіцієнти a_k і b_k залежать від параметрів і способа побудови схеми та від виду шукання вільних ліній. Відношення a_k/b_k зі зростанням k(відповідно функция φ_i зі зростанням Λ) для рівномірних схем повільно збільшується, а для ступеневих – помітніше зменшується.

Загальний метод розрахунку функцій φ_i поки відсутній. Але для більшості схем НВ можна отримати нескладні рекурентні співвідношення для обчислення функцій φ_i в двох крайніх точках при Λ→ 0 і Λ→ ∞. Це дозволяє знайти верхню і нижню оцінки втрат, які часто бувають досить близькими. Полегшує рішення задачі також можливість визначення функциї φ_iтільки для частини значень i. При функція φ_i настілько близька до 1, що її заміна на 1 не впливає на кінцевий результат. Величина i_rвизначається параметрами схеми та необхідною точністю розрахунків.