 |
|
Моделювання найпростішого потоку
Як було показано в розділі 2, в найпростішому потоці викликів з параметром l довжини інтервалів часу zi = ti – ti-1 >0 між послідовними викликами потоку розподілені за експоненціальним законом з тим же параметром 
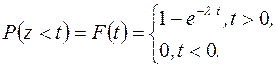 (8.2)
(8.2)
Ця обставина дозволяє сформувати процес надходження найпростішого потоку викликів на заданому проміжку часу за допомогою методу Монте-Карло. Згідно до вищеприведеної теореми, для одержання випадкових значень, що відповідають інтервалам між викликами, потрібно згенерувати послідовність псевдовипадкових чисел ri, для кожного з них розв’язати рівняння:
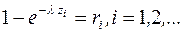 (8.3)
(8.3)
Розв’язуючи це рівняння відносно zi, маємо:
 . (8.4)
. (8.4)
Оскільки випадкові числа ri належать інтервалу [0, 1], то число (1 - ri), також є випадковим (із тим же рівномірним розподілом) з інтервалу [0, 1]. Тому для обчислення zi можна використовувати простішу формулу:
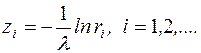 (8.5)
(8.5)
При цьому, якщо моделювання необхідно здійснити для проміжку часу [T1,T2], то час tk надходження чергового виклику найпростішого потоку слід визначати за співвідношенням:
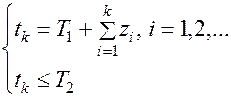 . (8.6)
. (8.6)
Результати прикладу імітаційного моделювання для найпростішого потоку з параметром представлено в таблиці 8.1.
Таблиця 8.1
Результати імітаційного моделювання
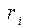
| 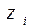
| 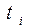
|
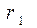
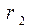 ...
...
| 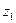
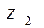 ...
...
| 
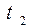 ...
...
|
Отримані значення можна перевірити на відповідність заданим умовам моделювання наступним чином. Весь інтервал моделювання [T1,T2] розбивається на кілька проміжків довжиною τ і підраховується кількість викликів Х(τ), що потрапили в кожний з інтервалів. Оскільки моделювався найпростіший потік, величина Х(τ) розподілена за законом Пуассона. Отже, можна висунути і перевірити, використовуючи відповідні статистичні критерії [5], гіпотезу про пуассонівський розподіл. Крім того, можна порівняти із заданим значенням параметра потоку λ значення параметра змодельованого потоку λмод , яке обчислити як відношення середнього значення кількості викликів в інтервалі до довжини цього інтервалу:
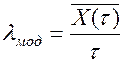 (8.5)
(8.5)
При досить близькому співпадінні λмод і λ моделювання можна вважати успішним.
Розглянутий підхід можна використовувати для імітації доволі широкого класу марківських розподілів випадкових величин, основаних на комбінації та змішуванні експоненціальних розподілів (див. п. 2.10). Ці величини можуть визначати інтервали між викликами, проміжки вільності й зайнятості джерела, повторення викликів, тривалості обслуговування. Як приклад розглянемо моделювання випадкової величини z з гіперекспоненціальним розподілом (2.49) при n = 3:
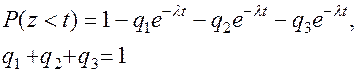 (8.6)
(8.6)
Для отримання послідовності значень необхідні два типи випадкових величин: Х – рівномірно розподіленої в інтервалі [0,1] та Z – експоненціально розподіленої з параметром λі . На початку кожного цикла генерується число х і перевіряється умова x < q1. При виконанні умови виробляється число z з параметром λ1 . Якщо перша умова не виконується, перевіряється наступна: x < q1+q2 . За разультатами перевірки виробляється число z з параметром λ2 при виконанні умови або λ3 у протилежному випадку.