 |
|
Незалежні похибки в сумі
Правила, які ми доки знайшли, можуть бути сформульовані коротко: коли вимірювані величини складаються або віднімаються, похибки додаються; коли вимірювані величини множаться або діляться, додаються відносні погрішності. У цьому і наступному розділах ми розглянемо, як за певних умов похибки, розраховані на підставі цих правил, можуть виявитися невиправдано великими. Точніше, ми побачимо, що якщо початкові похибки незалежні і випадкові, то реалістичніша (і менша) оцінка остаточної погрішності дається аналогічними правилами, в яких похибки (або відносні похибки) додаються квадратично (т. е. відповідно до процедури, яку ми незабаром визначимо).
Розглянемо спочатку обчислення суми q = х+у двох чисел х і у, які були виміряні звичайним способом:
(виміряне значення х) = хнайк ± Δх;
і аналогічно для у. Спосіб, який використовувався в останньому розділі, виглядав таким чином. По-перше, найкраща оцінка q = х + у є, очевидно, qнайк = xнайк + yнайк . По-друге, оскільки найбільші імовірніні значення для х і у рівні відповідно хнайк + Δх і yнайк + Δy, то найбільше імовірне значення величини q є
хнайк + yнайк + Δх + Δy (3.12)
Аналогічно, найменше імовірне значення q є:
хнайк + yнайк – Δх – Δy
Звідси ми робимо висновок, що величина q, ймовірно, лежитмежду цими двома значеннями, і похибка в q дорівнює
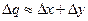
Щоб побачити, чому ця формула швидше за все переоцінює Δq, розглянемо, в якому випадку фактична величина q порівнюється з найбільшим значенням (3.12). Очевидно, це ожет статися, якщо ми недооцінили х на повну величину Δх і недооцінили у на повну величину Δу. Проте це дуже малоімовірно. Якщо х і у вимірюються незалежно і наші помилки випадкові за природою, в 50% випадків недооцінка х супроводжуватиметься переоцінкою у або навпаки. Тоді ясно, що імовірність недооцінки як х, так і у на повні величини Δх і Δу досить мала. Отже, значення 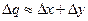переоцінює нашу можливу помилку.
А що ж тоді буде кращою оцінкою для Δq? Це залежить від того, що ми розуміємо під помилкою (т. е. що ми маємо на увазі, стверджуючи, що Δq "ймовірно", лежить десь між qнайк – Δq і qнайк + Δq . Це також залежить від того, які статистичні закони, яким підкоряються наші похибки у вимірах. У гл. 5 ми обговоримо нормальний розподіл, або розподіл Гауса, який описує виміри, схильні до випадкових похибок. Ми побачимо, що якщо виміри х і у виконуються незалежно і якщо вони обоє підкоряються нормальному розподілу, то похибка в q = х + у дається виразом
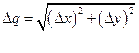(3.13)
Коли комбінують два числа, зводячи їх в квадрат, складаючи квадрати і потім витягаючи квадратний корінь, як в (3.13), то говорять, що числа додають квадратично. Таким чином, правило, яке міститься в (3.13), може бути сформульовано таким чином: якщо виміри х і у незалежні і схильні тільки до випадкових похибок, то похибка Δq в розрахованому значенні q = х + y дорівнює сумі квадратично доданих похибок Δх і Δу, або їх квадратичній сумі.
Важливо порівняти новий вираз (3.13) для похибки в q = х + y з нашим старим виразом
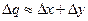(3.14)
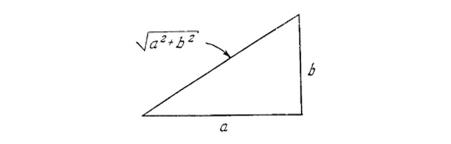
Мал. 3.2. Так як будь яка сторона трикутника менше двох інших сторін,
то завжди дійсна нерівність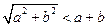 
По-перше, новий вираз (3.13) завжди менше, ніж старий (3.14), як можна бачити з простих геометричних міркувань. Для будь-яких двох позитивних чисел а і b числа а, b і 
відповідають трьом сторонам прямокутного трикутника (мал. 3.2). Оскільки довжина будь-якої сторони трикутника завжди менше суми двох інших сторін, то ясно, що 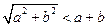і, отже, (3.13) завжди менше, ніж (3.14).
Оскільки вираз (3.13) для похибки в q = x+y завжди менше, ніж (3.14), то завжди, коли це можна, слід використовувати вираз (3.13). Проте воно не завжди правомірне. Вираз (3.13) відбиває можливість того, що переоцінка х може якось компенсуватися недооцінкою в у або навпаки. Легко можна навести приклад виміру, де така компенсація неможлива.
Припустимо, наприклад, що q = х + у є сума двох довжин х і у, виміряних однією і тією ж сталевою рулеткою. Припустимо також, що головне джерело похибки полягає в тому, що, як ми побоюємося, рулетка призначена для використання при температурі, що відрізняється від даної. Якщо ми не знаємо цієї температури (і не маємо надійної рулетки для порівняння), то ми повинні будемо визнати, що наша рулетка може бути довше або коротше, ніж її довжина, що калібрується, і що, отже, вона може давати недооцінені або переоцінені значення довжини. Цю похибку легко врахувати. Проте сенс полягає в тому, що якщо рулетка дещо довша, то ми недооцінюємо обидва значення х і у, а якщо рулетка дещо менша, то ми переоцінюємо обидва значення х і у. Таким чином, немає шансів для взаємної компенсації похибок, яка виправдовує використання квадратичної суми для обчислення похибки в q = х + у.
Пізніше (у гл. 9) ми доведемо, що незалежно від того, чи є наші помилки незалежними і випадковими, похибка в q = х + у не більше, ніж проста сума Δх + Δу :
Δq ≤ Δx + Δy (3.15)
тобто наш старий вираз (3.14) для Δq є насправді верхньою межею, яка справедлива в усіх випадках. Якщо у нас є які-небудь підстави підозрювати, що похибки в х і у не незалежні і випадкові (як в прикладі з виміром сталевою рулеткою), то використання квадратичної суми (3.13) для Δq не буде виправданим. З іншого боку, межа (3.15) гарантує, що Δq ясно не більше, ніж Δx + Δy, і надійнішим буде використання старого правила q є насправді верхньою межею, яка справедлива в усіх випадках. Якщо у нас є які-небудь підстави підозрювати, що похибки в х і у не незалежні і випадкові (як в прикладі з виміром сталевою рулеткою), то використання нами квадратичної суми (3.13) для Δq не буде виправданим. З іншого боку, межа (3.15) гарантує, що Δq ясно не більше, ніж Δx + Δy, і надійнішим буде використання старого правила.